Salut curieux! Suite à ton message je me suis dit j’ai tout faux, alors je vais me suicider, et puis la nuit est passée et j’ai trouvé une solution qui concilie ma théorie et tes données mais j’arrive à un truc de dingue, peut-être plus cohérent et qui colle à ce que j’avais un peu en tête, mais un truc de ouf, alors je vais suivre tes conseils et aller faire un séjour en hôpital psychiatrique. Porte-toi bien et portez-vous bien tous!curieux a écrit : 28 mars 2021, 19:38 L'accélérateur du LHC mesure un peu moins de 27 km de circonférence, les protons qui s'y déplacent font 11 245 tours par seconde pour atteindre une énergie de 14 tera eV, c'est un peu plus que 14 000 fois leur énergie de masse au repos.
Ce qui leur fait une vitesse légèrement inférieure à celle de la lumière.
27 km * 11 245 =~ 300 000 km/s c'est une mesure directe et donc une vitesse réelle, il n'y a aucune erreur possible d'interprétation.
Relativité, positivisme et réalisme
Re: Relativité, positivisme et réalisme
Re: Relativité, positivisme et réalisme
Oui! Je pensais que l‘hyper-sphère représentait le monde visuel (perçu par les ondes e.m.) et l’ hyper-plan le monde tangible, alors qu’ils correspondent respectivement au monde perçu (perçu par les sens) et à un monde invisible (que l’on ne perçoit pas) et portant présent.
Pour ce qui est de l’HP je vais d’abord aller voir un psychiatre avant d’y aller. Je verrais bien ce qu’il me dira.
Pour ce qui est de l’HP je vais d’abord aller voir un psychiatre avant d’y aller. Je verrais bien ce qu’il me dira.
Dernière modification par richard le 30 mars 2021, 17:54, modifié 1 fois.
Re: Relativité, positivisme et réalisme
Sûrement un signe ...richard a écrit : 29 mars 2021, 12:15Salut curieux! Suite à ton message je me suis dit j’ai tout faux, alors je vais me suicider, et puis la nuit est passée et j’ai trouvé une solution qui concilie ma théorie et tes données mais j’arrive à un truc de dingue, peut-être plus cohérent et qui colle à ce que j’avais un peu en tête, mais un truc de ouf, alors je vais suivre tes conseils et aller faire un séjour en hôpital psychiatrique. Porte-toi bien et portez-vous bien tous!

Re: Relativité, positivisme et réalisme
Garde tes sous, dans ton cas je vais te faire économiser 3 ans de consultations, la solution à ton problème est toute simple, quand t'étais jeune t'étais un jeune con et maintenant que t'es vieux , bein t'es un vieux con c'est aussi simple que ça.richard a écrit : 30 mars 2021, 12:08 Oui! Je pensais que l‘hyper-sphère représentait le monde visuel (perçu par les ondes e.m.) et l’ hyper-plan le monde tangible, alors qu’ils correspondent respectivement au monde perçu (perçu par les sens) et à un monde invisible (que l’on ne perçoit pas) et portant présent.
Pour ce qui est de l’HP je vais d’abord aller voir un psychiatre avant d’y aller. Je verrais bien ce qu’il me dira.
Le rôle de la physique mathématique est de bien poser les questions, ce n'est que l'expérience qui peut les résoudre. [Henri Poincaré]
- DictionnairErroné
- Messages : 4916
- Inscription : 15 mai 2019, 19:25
Re: Relativité, positivisme et réalisme
Ah bien là je peux ajouter quelque chose! Je parle par expérience, un con n'est pas une tare en soi, c'est de ne pas le savoir qui est problématique.curieux a écrit : 30 mars 2021, 23:34 quand t'étais jeune t'étais un jeune con et maintenant que t'es vieux , bein t'es un vieux con c'est aussi simple que ça.
La connaissance: Un ignorant qui sait qu'il est ignorant est bien moins ignorant qu'un ignorant qui ne sait pas qu'il est ignorant.
Re: Relativité, positivisme et réalisme
En fait le con c'est celui qui ne tient jamais compte des objections qu'on peut lui faire pour montrer l'incohérence de ses propos.
Plutôt que d'admettre qu'il s'est gourré il fera toutes sortes de pirouettes invraisemblables pour tenter de retomber sur ses pattes.
Voilà maintenant qu'il nous sort l'existence d'un monde invisible pour expliquer ses incohérences.
Plutôt que d'admettre qu'il s'est gourré il fera toutes sortes de pirouettes invraisemblables pour tenter de retomber sur ses pattes.
Voilà maintenant qu'il nous sort l'existence d'un monde invisible pour expliquer ses incohérences.
Le rôle de la physique mathématique est de bien poser les questions, ce n'est que l'expérience qui peut les résoudre. [Henri Poincaré]
Re: Relativité, positivisme et réalisme
Après avoir élaborécurieux a écrit : 31 mars 2021, 12:21 Voilà maintenant qu'il nous sort l'existence d'un monde invisible pour expliquer ses incohérences.
C’est très étrange. Merci en tout cas, curieux, de m’avoir aider sur cette voie.
Re: Relativité, positivisme et réalisme
alors monte ta secte et fout nous la paix avec tes prétentions scientifiques pauvre clown.
Le rôle de la physique mathématique est de bien poser les questions, ce n'est que l'expérience qui peut les résoudre. [Henri Poincaré]
Re: Relativité, positivisme et réalisme
Salut curieux! Je te remercie pour ce nouveau conseil, mais je ne sais pas si je pourrais réussir, je vais essayer, j’ai déjà exercé dans quatre domaines différents, je peux bien en tenter un cinquième.
Bon! Où en sommes-nous? Une réalité perceptible et une autre imperceptible. J’ai du mal à comprendre pourquoi la vitesse d’un corps ne peut dépasser celle de la lumière dans le monde perceptible. Ah si! fastoche E = γ m c2, l’énergie devient infinie quand la vitesse perçue vp atteint celle de la lumière c, et la vitesse imperceptible devient infinie.
Dès lors dans ce monde imperceptible la transmission d’informations peut être instantanée. Intéressant, non?
Bon! Où en sommes-nous? Une réalité perceptible et une autre imperceptible. J’ai du mal à comprendre pourquoi la vitesse d’un corps ne peut dépasser celle de la lumière dans le monde perceptible. Ah si! fastoche E = γ m c2, l’énergie devient infinie quand la vitesse perçue vp atteint celle de la lumière c, et la vitesse imperceptible devient infinie.
Dès lors dans ce monde imperceptible la transmission d’informations peut être instantanée. Intéressant, non?
Re: Relativité, positivisme et réalisme
La vitesse et le temps ne sont-ils pas liés ?
Русский военный корабль, иди нахуй ! 
Re: Relativité, positivisme et réalisme
Ouais frérot.richard a écrit : 01 avr. 2021, 11:20 Salut curieux! Je te remercie pour ce nouveau conseil, mais je ne sais pas si je pourrais réussir, je vais essayer, j’ai déjà exercé dans quatre domaines différents, je peux bien en tenter un cinquième.
Bon! Où en sommes-nous? Une réalité perceptible et une autre imperceptible. J’ai du mal à comprendre pourquoi la vitesse d’un corps ne peut dépasser celle de la lumière dans le monde perceptible. Ah si! fastoche E = γ m c2, l’énergie devient infinie quand la vitesse perçue vp atteint celle de la lumière c, et la vitesse imperceptible devient infinie.
Dès lors dans ce monde imperceptible la transmission d’informations peut être instantanée. Intéressant, non?
Mais t'as pensé au fait que le temps de ce monde imperceptible et le nôtre pourraient ne pas coïncider ?
Re: Relativité, positivisme et réalisme
Salut Akine! J’ai posé que c’est le même écoulement du temps dt, donc le même temps:
v = dx/dt; vp = dxp/car pour moi au départ c’etait le même monde, le monde visuel d’un côté et le monde tangible de l’autre. Mais curieux m’a ouvert les yeux sur d’autres mondes. Merci qui? Merci curieux!
Alors je vais réfléchir à ta question, mais à priori je ne vois pas pourquoi ce ne serait pas le même temps.
v = dx/dt; vp = dxp/car pour moi au départ c’etait le même monde, le monde visuel d’un côté et le monde tangible de l’autre. Mais curieux m’a ouvert les yeux sur d’autres mondes. Merci qui? Merci curieux!
Alors je vais réfléchir à ta question, mais à priori je ne vois pas pourquoi ce ne serait pas le même temps.
Re: Relativité, positivisme et réalisme
Alors, tu sais quoi ?richard a écrit : 01 avr. 2021, 18:41 Salut Akine! J’ai posé que c’est le même écoulement du temps dt, donc le même temps:
v = dx/dt; vp = dxp/car pour moi au départ c’etait le même monde, le monde visuel d’un côté et le monde tangible de l’autre. Mais curieux m’a ouvert les yeux sur d’autres mondes. Merci qui? Merci curieux!
Alors je vais réfléchir à ta question, mais à priori je ne vois pas pourquoi ce ne serait pas le même temps.
Mettons que par exemple tu aies un référentiel à partir duquel tu choisisses de déterminer les autres.
Si les temps de deux mondes sont différents, vu que les événements arrivent à la fois dans l'un et dans l'autre, il faut que chaque référentiel qu'on choisit dans l'un ou l'autre monde inclue non seulement trois axes de position, mais aussi un axe de temps et un instant de référence, non ?
Mettons que dans le monde "fondamental" non-illusoire, il n'y ait pas de limite à la vitesse. Mettons également que dans ce même monde, les vitesses s'additionnent normalement, comme dans un espace-temps de Galilée.
C'est bien comme cela que tu l'as construit ?
Eh bien, quand un événement survient à un certain temps et en un certain lieu pour un certain référentiel du monde illusoire (celui de la RR), il doit survenir aussi en un certain temps et en un certain lieu du monde non-illusoire (celui de la relativité richardienne). Logique.
Si je me place dans un ET à deux dimensions (t et x) pour simplifier les choses, cela veut dire qu'à chaque couple (T,X) de l'espace-temps non-illusoire correspond un couple précis (t,x) de l'espace-temps illusoire. Il y a donc une relation bijective entre les deux ET.
Est-ce que tu saurais trouver cette relation F telle que F((T,X))=(t,x) pour que le monde illusoire soit compatible avec la RR et ses observations ?
(Moi, oui. Mais je te laisse chercher.)
Re: Relativité, positivisme et réalisme
Salut Akine! Bon! D’abord je n’ai pas de référentiel.Akine a écrit : 02 avr. 2021, 08:24 Mettons que par exemple tu aies un référentiel à partir duquel tu choisisses de déterminer les autres.
Non!Si les temps de deux mondes sont différents, vu que les événements arrivent à la fois dans l'un et dans l'autre, il faut que chaque référentiel qu'on choisit dans l'un ou l'autre monde inclue non seulement trois axes de position, mais aussi un axe de temps et un instant de référence, non ?
Pas toutafè, dans le monde non-illusoire, le monde perceptible —celui que nous percevons, dans lequel nous vivons— les vitesses perçues s’additionnent comme en RR, elles sont limitées par la vitesse de la lumière, par contre dans le monde caché, imperceptible, les vitesses s’additionnent « normalement », elles ne sont pas limitées.Mettons que dans le monde "fondamental" non-illusoire, il n'y ait pas de limite à la vitesse. Mettons également que dans ce même monde, les vitesses s'additionnent normalement, comme dans un espace-temps de Galilée.
C'est bien comme cela que tu l'as construit ?
ce que tu appelles le monde non-illusoire est le monde que nous percevons, le monde illusoire est un monde auquel nous n’avons pas accès.[Eh bien, quand un événement survient à un certain temps et en un certain lieu pour un certain référentiel du monde illusoire (celui de la RR), il doit survenir aussi en un certain temps et en un certain lieu du monde non-illusoire (celui de la relativité richardienne). Logique.
Je cherche comment les appeler monde/univers/réalité/réel ? Perceptible d’un côté, caché de l’autre?
comme je te l’ai dit je n’ai pas d’espace-temps. Je n’ai que deux espaces, un qui décrit le monde (l’univers) perceptible et un autre qui décrit le monde caché; il n’est pas illusoire, il ne nous est pas directement accessible.Si je me place dans un ET à deux dimensions (t et x) pour simplifier les choses, cela veut dire qu'à chaque couple (T,X) de l'espace-temps non-illusoire correspond un couple précis (t,x) de l'espace-temps illusoire. Il y a donc une relation bijective entre les deux ET.
Un changement d’observateur (ce que l’on appelle un changement de référentiels en RR) se fait simplement par changement d’origine dans les deux espaces.
- DictionnairErroné
- Messages : 4916
- Inscription : 15 mai 2019, 19:25
Re: Relativité, positivisme et réalisme
Malgré que je n'y comprends pas grand-chose, c'est tout de même fascinant de réaliser que la relativité ne peut être comprise et expliquer que par des modèles mathématiques. Le sens provient des chiffres et non des mots, moi, ça me fait tripper!

ou ceci:
L'accélérateur de particules le plus puissants du monde est au coeur d'une potentielle découverte qui pourrait, si elle se confirme, bousculer le modèle connu de la physique. En se désintégrant, il est admis que les particules composites émettent en probabilité égale des particules élémentaires: électrons, muons et taurons. Mais ici, en désintégrant des mésons B, l'apparition d'électrons était favorisée, suggérant l'existence de nouvelles particules à l'oeuvre ou d'interactions inconnues.
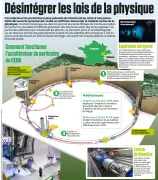
ou ceci:
L'accélérateur de particules le plus puissants du monde est au coeur d'une potentielle découverte qui pourrait, si elle se confirme, bousculer le modèle connu de la physique. En se désintégrant, il est admis que les particules composites émettent en probabilité égale des particules élémentaires: électrons, muons et taurons. Mais ici, en désintégrant des mésons B, l'apparition d'électrons était favorisée, suggérant l'existence de nouvelles particules à l'oeuvre ou d'interactions inconnues.

La connaissance: Un ignorant qui sait qu'il est ignorant est bien moins ignorant qu'un ignorant qui ne sait pas qu'il est ignorant.
Re: Relativité, positivisme et réalisme
Je ne vois pas ce qui te fait croire ça.DictionnairErroné a écrit : 02 avr. 2021, 14:26 ... c'est tout de même fascinant de réaliser que la relativité ne peut être comprise et expliquer que par des modèles mathématiques. Le sens provient des chiffres et non des mots, moi, ça me fait tripper!
La relativité peut très bien être expliquée avec des mots et c'est ce qu'Einstein a fait avec ce livre:
https://www.babelio.com/livres/Einstein ... ivite/5639
Re: Relativité, positivisme et réalisme
En résumé et grâce à vos remarques, en particulier celles de curieux, je dirais donc qu'il y a un monde perceptible de structure sphérique, et un monde imperceptible de structure euclidienne. Tous les deux ont six dimensions, trois d’espace et trois de vitesse. Les grandeurs imperceptibles et perceptibles sont liées par le coefficient de Lorentz γ:
les longueurs Li = γ Lp, les vitesses vi = γ vp, les forces Fp,t= mp gp,t, Fi = γ mi gi,t, l’indice t a trait à la tangente à la trajectoire du corps. La formule pour l’acceleration normale imperceptible est différente, la masse imperceptible n’est sûrement pas constante, mais il faut prendre ça avec des pincettes pour les forces car je n’ai pas encore bien exploré la dynamique. Il faut aussi que je détermine la fonction holomorphe qui relie ces deux mondes même si j’ai une petite idée il faut que je la confirme.
les longueurs Li = γ Lp, les vitesses vi = γ vp, les forces Fp,t= mp gp,t, Fi = γ mi gi,t, l’indice t a trait à la tangente à la trajectoire du corps. La formule pour l’acceleration normale imperceptible est différente, la masse imperceptible n’est sûrement pas constante, mais il faut prendre ça avec des pincettes pour les forces car je n’ai pas encore bien exploré la dynamique. Il faut aussi que je détermine la fonction holomorphe qui relie ces deux mondes même si j’ai une petite idée il faut que je la confirme.
Re: Relativité, positivisme et réalisme
Pas des modèles très élaborés toutefois. Il suffit :DictionnairErroné a écrit : 02 avr. 2021, 14:26Bien que je n'y comprenne pas grand-chose, c'est tout de même fascinant de réaliser que la relativité ne puisse être comprise et expliquée que par des modèles mathématiques.
- de savoir, d'une part, calculer (par exemple) le temps pour parcourir 600 m à la vitesse moyenne de 30 m/s
- de savoir, d'autre part, que quelque soit le référentiel R0 (train, fusée, maison...) non accéléré (ou presque) dans lequel on est immobile :
- 1/ la vitesse mesurée de la lumière y vaut c,
. - 2/ les objets subissent une contraction (dite de Lorentz) si on les met au repos dans un mobile R1 se déplaçant à vitesse constante v par rapport au référentiel R0 dans lequel on est immobile.
. - et que 3/
- deux points A et B de notre référentiel R0,
- équidistants de la source I d'un flash lumineux,
- reçoivent le flash lumineux en même temps (forcément puisque le temps de parcours est le même).
- le temps que met la lumière pour faire l'aller-retour entre deux miroirs immobiles A et B c'est la distance d'aller-retour divisé par cette vitesse c
. - le temps que met la lumière pour faire l'aller-retour entre deux miroirs A et B, tous les deux en mouvement à la même vitesse v, est mesuré comme valant c par un observateur allant lui aussi à la même vitesse v (forcément puisqu'il utilise ce type de temps d'aller retour pour mesurer cette durée)
. - un même objet est mesuré plus court quand il est en mouvement à vitesse v. Il est contracté par la contraction de Lorentz (en (1-v²/c²)^(1/2))
. - avec ça, un calcul simple (de type durée = distance divisée par vitesse) montre que le temps mis par la lumière pour faire l'aller-retour :
- entre deux miroirs A et B en mouvement à la vitesse v,
- reliés par une tige de longueur L0 quand elle est au repos,
- donc de longueur L = L0(1-v²/c²)^(1/2) à cause de la contraction de Lorentz,
- est égal à (2L0/c)/(1-v²/c²)^1/2.
Re: Relativité, positivisme et réalisme
Salut le dico! Laisse béton la relativité einsteinienne. Dans icelle le temps propre, donc le temps réel s’écoule de la même manière dans tous les référentiels et en même temps les durées dépendent de la vitesse du corps observé. Avec trois vaisseaux spatiaux il est impossible de déterminer l’ecoulement du temps dans chacun des vaisseaux en fonction de leur vitesse respective.
Re: Relativité, positivisme et réalisme
Ci-dessous un petit exercice de comparaison entre relativité einsteinienne versus richardienne
Combien de temps met un léopard, courant à la vitesse de 30 m/s, pour attraper une gazelle, située à 60m de distance, s'enfuyant à la vitesse de 20m/s
1/ en relativité einsteinienne
2/ en relativité richardienne
En déduire la plus grande probabilité de survie du léopard en relativité richardienne...
...et donc l'incontestable pertinence de cette théorie d'une grande audace scientifique, eu égard à l'existence, factuelle, toujours actuelle, prouvée, de cette espèce animale.
Attention toutefois, les faits n'ont pas toujours raison. En projection stéréographique hypersphérique à compactification d'Alexandrov inversée, le son peut rattapper un avion volant à vitesse supersonique. Bien que ce soit un fait, il s'avère que l'apparence n'est pas systématiquement conforme à cette réalité pourtant incontestable (elle découle du fait que, comme chacun sait, le temps est absolu).
Re: Relativité, positivisme et réalisme
Ben oui! Même en relativité einseinienne le temps est absolu. Einstein a réussi à faire croire à des gens qu’il était relatif! Vachement fort cet Einstein!
Re: Relativité, positivisme et réalisme
Heureusement que tu es là avec une théorie des objets en mouvement absolu immobile pour corriger tout ça (en relativité hypersphérique à compactification d'Alexandrov inversée).richard a écrit : 03 avr. 2021, 14:08Ben oui! Même en relativité einseinienne le temps est absolu. Einstein a réussi à faire croire à des gens qu’il était relatif! Vachement fort cet Einstein!
Re: Relativité, positivisme et réalisme
Si tu lisais mes messages tu verrais qu’ils ne sont pas immobiles; ils ont même deux vitesses, alors tu vois toi avec ta vitesse unique t’es un peu ridicule. 
Qui est en ligne ?
Utilisateurs parcourant ce forum : Aucun utilisateur inscrit