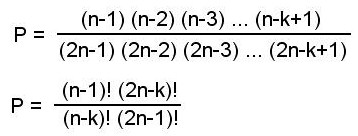Salut à tous ceux qui ont participé à cette enfilade.
Dans le temps où j'en avais, je disais souvent à mes étudiants que résoudre un problème d'analyse combinatoire (le problème de Chiwaw en est un) c'est un peu comme
défaire un noeud de ficelle. On peut faire glisser une boucle avant ou après une autre : en fin de compte, ça revient au même.
Il y a souvent plusieurs solutions équivalentes (i.e. plusieurs façons correctes d'arriver à la réponse correcte). La meilleure solution n'est pas nécessairement la plus simple, ni la plus courte. C'est plutôt
celle où l'on voit le mieux qu'on ne se trompe pas.
Je pense que, parmi toutes les réponses correctes qu'on a trouvées, la plus simple est probablement celle de Hallu (qui est probablement aussi celle de Zwielicht). Celle de Ptoufle la chauffe de près. J'admets que ma première solution (via la loi hypergéométrique) était "inutilement forte". Un peu comme sortir la grosse souffleuse pour déblayer 1 cm de neige.
La solution de Raphy était peut-être encore plus simple que celle de Hallu, mais elle avait le gros défaut d'être incorrecte.
Le problème de Chiwaw peut être généralisé en remplaçant son 3 et son 5 par k et n.
On a 2n cartes, parmi lesquelles k sont de type B et (2n-k) sont de type A (avec k ≤ n). On brasse ces cartes et on en fait deux piles de n cartes chacune.
La probabilité que les k cartes de type B soient dans la même pile est alors :
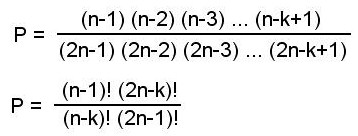
Ces deux formules, algébriquement équivalentes, s'obtiennent à la fois par la méthode de Hallu, par la méthode de Ptoufle et par la grosse souffleuse hypergéométrique.
Avec n=5 et k=3 (le cas de Chiwaw), elles donnent P = 1/6.
Avec, par exemple, n=26 et k=13 (13 cartes de coeur parmi 52 cartes), elles donnent P = 0.000032757.
Quand on partage au hasard
un jeu de 52 cartes en deux piles de 26, on a donc environ une chance sur 30528 que les 13 cartes de coeur se trouvent dans la même pile.

Denis
P.S. À moins, évidemment, que je me sois trompé dans mes calculs, ce qui n'est pas absolument absolument absolument impossible.
Les meilleures sorties de route sont celles qui font le moins de tonneaux.