Forum Sceptique

Salut Mireille,

Tu demandes :

pourrais-tu devenir un Alchimiste (?)

Non.

Pour te faire plaisir, j'accepterais de devenir (provisoirement) un âne ou un navet, mais certainement pas un alchimiste. C'est trop bas.

Plus sérieusement, à la réponse de Brigand, j'ajoute l'explication suivante :

Dans la seconde formule, j'ai tracé quelques barres rouges (notées C3, C5, C7 et C9).

.

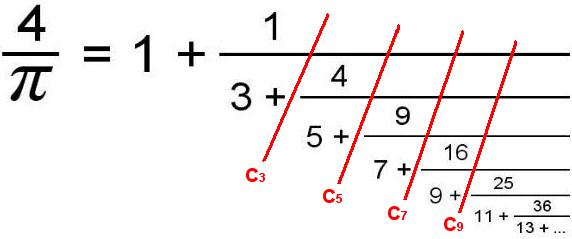La barre C3 nous fait arrêter le calcul après le 3. Dans ce cas, on ne calcule que 1 + 1/3 = 4/3 ≈ 1.3333333333.

Si on arrête le calcul après le 5 (i.e. à la barre C5), on obtient 1 + 1/(3 + 4/5) = 1 + 1/(19/5) = 24/19 ≈ 1.2631578947.

Si on arrête après le 7, après simplification, on obtient la fraction 51/40 = 1.275.

Si on arrête après le 9, on obtient 555/436 ≈ 1.2729357798.

Si on arrête après le 13 on obtient, après simplification, 3220/2929 ≈ 1.2732305259.

Ce que l'équation dit, c'est que, si on ne coupe jamais le calcul, on obtient exactement 4/π ≈ 1.27323954473516268615...

On peut constater que, quand on a coupé après le 13, on avait déjà 5 décimales correctes. Si on avait voulu avoir un milliard de décimales correctes, on n'aurait eu qu'à couper suffisamment loin.

Concernant l'autre "perle",



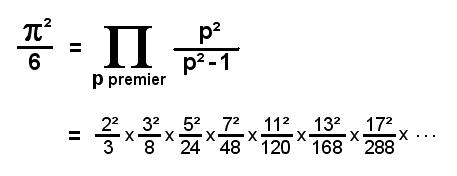
je devine que ton problème en est un de "lecture des notations". Je suis bien certain que tu sais ce qu'est un nombre premier. Ce sont les nombres 2, 3, 5, 7, 11, 13, 17, etc.

Ce que la formule dit c'est que si on calcule le produit de ce que vaut p²/(p²-1), quand p vaut successivement 2, 3, 5, 7, 11, 13, 17, ... , ce produit (d'une infinité de termes) vaut exactement π²/6 ≈ 1.6449340668482264364724...

Dans la ligne du bas de la formule, on indique les premiers termes du produit. Par exemple, le nombre premier "p = 7" fournit un p²/(p²-1) qui vaut 7²/(7²-1) = 49/48. On peut aisément constater que si on "coupe" le calcul après seulement 5 termes, on obtient (4/3)x(9/8)x(25/24)x(49/48)x(121/120) = 29645/18432 ≈ 1.60835. La convergence est moins rapide que dans le cas de l'autre formule, mais c'est déjà pas mal près du "but" 1.64493... . Si on avait souhaité obtenir π²/6 avec un zilliard de décimales correctes, il aurait suffi de tronquer le calcul suffisamment loin (en incluant plus de nombres premiers).

Bon. J'espère que c'est plus clair qu'avant.

Pour les autres, désolé pour le gros hors-sujet. J'espère qu'il ne vous a pas coupé l'inspiration.

Denis

Salut Denis,

Denis a écrit :Ce que la formule dit c'est que si on calcule le produit de ce que vaut p²/(p²-1), quand p vaut successivement 2, 3, 5, 7, 11, 13, 17, ... , ce produit (d'une infinité de termes) vaut exactement π²/6 ≈ 1.6449340668482264364724...

J'ai un peu de mal avec celle là. Il me semblait qu'on n'avait pas de formule pour calculer les nombres premier, qu'on était obligé de tester des nombres candidats... alors comment arrive on à affirmer connaitre le résultat d'une opération impliquant des nombres qu'on ne connait pas ???

Tes perles sont elles des conjectures ou ont elles été démontrées ?

Salut Étienne,

Tu dis :

alors comment arrive on à affirmer connaitre le résultat d'une opération impliquant des nombres qu'on ne connait pas ???

Tes perles sont elles des conjectures ou ont elles été démontrées ?

C'est démontré. Dans le cas de celle avec les nombres premiers, la preuve (due à Euler) remonte à presque 3 siècles.

La partie difficile était de montrer que la somme des inverses des carrés vaut (exactement) π²/6 .



Une fois ce résultat établi, montrer que la somme des inverses des carrés peut s'exprimer sous la forme du produit (sur tous les nombres premiers p) de p²/(p²-1) n'est pas très difficile.

Sans entrer dans les détails, l'idée principale se base sur le fait que tout nombre entier n s'exprime de façon unique sous la forme de produit de puissances de nombres premiers.

Par exemple, 28 = 22x30x50x71x110x130...

Au nombre 28 correspond donc la suite d'exposants 2, 0, 0, 1, 0, 0,...

Inversement, à toute suite d'exposants k1, k2, k3, k4... (se "terminant" par des zéros) correspond un et un seul entier n.

Par exemple, à la suite 0, 2, 1, 0, 3, 0, 0, ... correspond l'entier 20x32x51x70x113 = 59895.

En remplaçant une somme sur tous les entiers n de, disons, F(n), par une une somme sur toutes les suites k1, k2, k3, k4, ... de F(p1k1xp2k2xp3k3...), tout ce qu'on fait, c'est sommer tous les F(n) dans un autre ordre. Sommer dans un autre ordre ne change pas la somme.

Bien sûr, il reste quelques petites passes algébriques élémentaires (comme remplacer une somme de produits par un produit de sommes), mais il n'y a rien de magico-transcendant dans ces opérations.

Si c'était vraiment difficile, ça ne serait pas connu depuis presque 3 siècles.

Denis

Merci, c'est pas mal plus clair maintenant.

Salut Brigand et Denis,

Je vais prendre le temps de regarder ce que vous m'avez apporté.

Pour répondre à la question de Denis, je n'y comprends pas grand chose en nombre premier, mais je cuisine admirablement les piments farçies. Si un jour vous avez envie de faire une surprise à votre Douce, n'hésitez pas à me demander comment les cuisiner.

Denis,

Je comprends que pour me faire cette petite démonstration imagée tu as préfféré être un Navet provisoire plutôt qu'un Alchimiste, bien sûr ça refroidit mes ardeurs de femme en mal d'arithmétiques, mais ça permet d'y voir plus clair

Merci !

Salut Denis!


Je suis aussi admiratif des résultats mathématiques. J'ai vraiment l'impression de découvrir une sorte d'univers platonicien lorsque je suis plongé dans une activité mathématique.

Bien que tu aies sûrement raison, je t'avoue être curieux de connaitre ce qui te fait pencher en faveur de la mortalité de la danse des idées. Dans quel sens emploies-tu le terme « mortelle » (à part le fait qu'il est très dangereux de danser sur des idées)?


Cordialement.

Salut Dave,

Tu dis :

je t'avoue être curieux de connaitre ce qui te fait pencher en faveur de la mortalité de la danse des idées.

Candidement j'estime que, parmi les arguments "pour" la mortalité de la danse des idées, un des plus costauds est celui qui s'appuie sur le fait qu'une grave désorganisation du cerveau a tendance à provoquer une grave désorganisation de la danse des idées. Par exemples, l'Alzheimer ou les traumatismes crâniens.

Il me semble naturel d'en conclure qu'une désintégration complète du cerveau devrait provoquer un effacement complet de la danse des idées. Aussi absolu que celui d'avant la vie de l'animal concerné.

Grosso modo.

Denis

Salut Denis!


Je ne sais pas si j'ai bien compris, mais, dans cette optique que vous évoquez, à part l'univers lui-même (et encore), quelles sont les choses qui pourraient être considérées comme immortelles?

Salut Dave,

Tu dis :

à part l'univers lui-même (et encore), quelles sont les choses qui pourraient être considérées comme immortelles?

Pour "immortel", je ne vois pas d'exemple, mais pour "intemporel", je propose les "objets" mathématiques, comme le théorème de Pythagore, la table de multiplication et l'ensemble de Mandelbrot.

Si on considère que "mourir", c'est "cesser de vivre", alors, au sens strict, ce qui est immortel est nécessairement vivant. Ça limite grandement le nombre de candidats.

Bien sûr, si on étire le sens du mot "mourir" et qu'on le prend au figuré, dans un sens voisin de "cesser d'exister", alors ça ouvre la porte à des candidats non-vivants, comme les cailloux et les photons.

Mais même là, je suis loin d'être convaincu que quoi que ce soit d'existant le soit pour toujours.

Peut-être, comme tu le mentionnes, l'Univers dans son entièreté, à moins d'un Big Crunch ou que le temps lui-même s'épuise avant lui.

Denis

Salut Denis!


Il est intéressant que tu fasses une distinction entre « immortel » et « intemporel ». Si je comprends bien, un objet mathématique est mortel, mais intemporel. En y ayant déjà quelque peu réfléchi, je peux assez bien m'imaginer cette possibilité, bien que ça puisse être contre-intuitif, puisqu'on a tendance à voir la mortalité comme une fin à l'intérieur même du temps. D'ailleurs, les exemples que tu donnes semblent aller dans le sens de cette vision.

Aussi, c'est toujours fascinant de voir un objet mathématique (en l'occurrence, une fractale) si simple dans sa définition et si joli dans sa représentation, mais si complexe dans son élaboration algébrique et algorithmique.

Enfin, merci pour ces précisions.

Salut Dave,

Tu dis :

Il est intéressant que tu fasses une distinction entre « immortel » et « intemporel ». Si je comprends bien, un objet mathématique est mortel, mais intemporel.

Non. Pas vraiment. Un objet mathématique n'est pas plus mortel qu'immortel, puisqu'il n'est pas vivant. L'ensemble de Mandelbrot n'est pas vivant. Parler de sa mort n'a aucun sens.

J'ai l'impression que tu prends "immortel" dans le sens figuré de "éternel vers le futur". Si on veut avoir des chances d'y voir un peu clair, il faudrait distinguer ces deux idées et n'appliquer "immortel" (ou "mortel") qu'à ce qui est vivant.

Quand à l'éternité (vers le futur ou ouverte aux deux bouts), elle ne s'applique pas aux machins intemporels où le temps (en secondes) ne joue pas plus que la masse (en kg) ou la longueur (en mètres). Quelle est la masse d'un machin abstrait?

Je veux bien admettre qu'une éternité figée soit proche d'une intemporalité puisque le temps y devient un paramètre inutile. Je considère toutefois que si ma danse des idées se continuait dans l'au-delà, ce serait dans une éternité (ouverte aux deux bouts ou seulement vers le futur) qui serait non figée, sinon ça serait une bien drôle de danse.

Une danse figée?

Denis

Salut Denis!


Il me semblait bien que j'avais mal compris. Lorsque tu as dit « ma danse des idées est mortelle », j'ai fait le raccourci suivant : « les idées sont mortelles ». C'est pour cela que je cherchais à comprendre le sens que tu attribuais à ce terme. Je pensais, à ma grande surprise, que c'était une élaboration philosophique inédite.

Si je comprends bien, c'est bien cette admiration (la danse) et la compréhension (peu importe de l'objet finalement, qu'il soit mathématique ou non) que l'on ressent par rapport à quelque chose qui sont mortelles? Si c'est cela, oui, ça me semble assez clair et évident maintenant. La façon que l'on ressent, que l'on comprend une chose dépend d'une structure (notre cerveau en l'occurrence) qui, elle, demeure provisoire, changeante, instable (à long terme du moins). Pour moi, cela va de soi et ce n'est ainsi pas nécessaire de le mentionner. Mais, je peux comprendre aussi qu'on le mentionne, puisqu'une grande quantité de gens encore aujourd'hui (malgré les études scientifiques allant dans le sens contraire) croient que leur mémoire des êtres qu'ils ont aimés (par exemple) restera intacte dans l'au-delà.

Quant à l'aspect intemporel des objets mathématiques en eux-mêmes, si je comprends bien, c'est simplement une façon de dire qu'ils ne dépendent pas à priori d'un paramètre « temps » (ni même d'un paramètre « espace »). Pour moi, c'est encore une fois assez évident. Mais, étonnamment, j'ai connu une personne qui doutait fortement du caractère irrationnel de « pi » en se basant sur la physique quantique. Il était aussi persuadé de l'existence d'un caractère contradictoire à la base des mathématiques (alors qu'il n'y a rien de moins contradictoire que les objets mathématiques à mon sens) en croyant que l'ensemble vide était mal défini. C'était assez exaspérant.

Cependant, des questions philosophiques (bien que surement inutiles) du genre : « est-ce qu'il existe une logique universelle (le projet de Leibniz)? » ou « est-ce que les objets mathématiques abstraits ont une existence réelle dans un monde platonicien? » sont moins évidentes à trancher, je trouve.

Eternité: sans début ni fin, ce qui n'implique pas forcément l'idée d'une droite. Vue sous forme d'un huit couché, l'éternité "en mouvement" peut être d'un côté, (la droite du huit) hors la durée et de l'autre, dans la durée*. Le nombre en mouvement ou nombré peut alors être conçu comme "intemporel" ou potentiel et (sur le côté gauche) ou "temporel" ou représentant l'idée de ce qui est tangible, palpable.

ps: *durée et non temps.

Message édité pour cause d'incapacité chronique à faire une citation correcte.