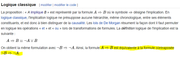
Sur papier oui. Quand on fait de la logique formelle ou des math, c’est implacable.Etienne Beauman a écrit : 14 août 2022, 11:13Il en reste que les deux formulations de Richard veulent dire exactement la même chose.
Sauf que traduit dans « d’autres sphères », comme dans celle qui comporte des aspects qui nous importent et d’autre moins, de façon pragmatique en tant qu’être humains, l’important n’est parfois plus l’implacabilité logique ou numérique. Par exemple, lorsque je partage une pizza en deux parts égales pour moi et l’un de mes potes, quand bien même tu viendrais nous démontrer que l’une des pointes comporte un microgramme de plus que l’autre, nous allons quand même considérer et accepter que je l’ai partagé de façon « égale » et que toi tu encules les mouches pour un détail qui n’apporte rien, qui n’ajoute aucune « plus value » utile à ce qui nous importe dans ce cadre spécifique.
Dans ce cas n-1µg ≠ n est exact sur papier, sans toutefois invalider que Dash a partagé la pizza en deux pointes de taille égale.
Idem avec : « Si j'observe quelque chose, alors il existe. Si quelque chose n'existe pas, je ne peux pas l'observer. »
C’est logique et valide, car ça ne fait référence à rien d’autre que des rapports logiques intrinsèques dans un « vase clos », soit : a->b <-> non b->non a
Oui! Sauf que la première phrase — traduite dans le présent contexte de la discussion — est fausse (à ne pas confondre avec « valide »)!
Parce que ce « vase clos » de logique formelle ne comporte pas la « dimension interprétation » qui peut être présente hors de ce vase clos. Ou alors il faut l’inclure et la traduire expressément comme tu l’as fait ensuite ici :
« Si je crois observer X, alors il existe Y que j'interprète en une observation de X. »
Ce qui revient, en langage naturel, à faire exactement ce que j’ai souligné et partagé à richard en lui écrivant :
« Pour la première, ce n’est pas que ce que tu observes n’a pas lieu ou cours (il y a bien une manifestation observée), mais ton interprétation de ce que c’est n’est pas forcément égale à ce que tu crois~interprètes qui existe ».
Ce qui, oui — maintenant qu’est inclus « Y » (la notion d’interprétation~croyance) dans la formulation —, sur papier, rend la phrase équivalente à (sa contraposée) :
« Si Y n'existe pas, alors je ne peux croire à l'observation de x »
En effet!
Mais uniquement a posteriori parce qu’on vient d’inclure « Y » qui prend la valeur « interprétation~croyance ». Sauf que sans avoir conscience de « Y » et/ou oublier la possibilité de « Y » résulte que l’on ne peut même pas formuler cette phrase~implication logique!
Mon objectif étant justement de souligner, de rappeler à richard qu’ « Y » était une possibilité à ne pas négliger~oublier (une « disjonction non-exclusive » si l’on veut qui s’ajoute à « b » comme possibilité, soit « b » ou « Y »). Alors pour ce qui nous importe dans la discussion, tant que n’était pas inclus cette possibilité, l’on ne peut pas être d’accord avec la première formulation sans « Y » de Richard pour ensuite, a posteriori, dire que parce que celle avec l’ « Y » peut être équivalente à sa propre contraposée sur papier, que celle sans « Y » est « vrai ». Car même si elle est valide logiquement, le fait qu’elle soit fausse par son omission d’une autre possibilité que « b » suffit à justifier le désaccord (hors du vase clos de la logique formelle).
Alors que pour la 2e phrase à savoir que « Si quelque chose n’existe pas, on ne peut pas l’observer. ». Elle demeure valide et vraie dans tous les cas et « vases »!
A
Bref, je te laisse tenter de reformaliser ça correctement puisque, toi, c’est manifestement ce qui t’intéresse! 
