Forum Sceptique

@Dash

Reste à savoir quel degré d’imprécision tolère un système neurobiologique.
La conformation spatiale d’une protéine et sa trajectoire jusqu’à un récepteur (la base de la biologie) peuvent également tolérer une part d’imprécision (comme la balle de golf et le trou).

La position exacte de la balle, l’adhérence/elasticité du terrain, le vent, la température, il n’y a pas que le coup qui entre en compte.

Ça n’apporte rien au débat.

Dash a écrit : 22 févr. 2021, 16:47 Autrement dit, ce que nous nommons « causalité » n'est possible qu'à cause de l'imprécision qui importe en fonction de ce que l'on observe et veut reproduire, mais dans les faits, puisque rien ne se reproduit de façon parfaitement identique 2 fois de suite, ben c'est qu'il n'y a pas de causalité effective dans les faits dans l'univers Comme le suggère ABC, la causalité n'est qu'un outil!

Attention Dash, tu te fais contaminer par la propagande de Dany, le principe de causalité, c'est la cause précède l'effet, rien d'autre. et dans l'expérience du billard il est bien respecté, un joueur tape dans la boule avant qu'elle ne tombe dans le trou.
C'est le déterminisme : même cause ==> même effet qui n'est probablement qu'une illusion du à l'observateur macroscopique, quand abc parle d'expérience semblant violer le principe de causalité il parle d'expérience où de notre point de vue conditionné par la flèche du temps allant du passé vers le futur, l'effet aurait lieu avant sa cause.

Totolaristo a écrit : 22 févr. 2021, 15:00
(Si vous maintenez que la causalité peut faire émerger de l’indéterminé, il va falloir en apporter la preuve. Déjà parce que c’est fatigant que vous ne l’ayez pas fait, et aussi parce que ça serait révolutionnaire.)

Tu poses encore cette même question. Regardons du côté des mathématiques.

Il y a une fonction dans le tabulateur Excel qui génère des nombres aléatoires.

*****************************************************************************
«ALEA (ALEA, fonction)
ALEA renvoie un nombre réel aléatoire distribué de manière symétrique supérieur ou égal à 0 et inférieur à 1. Un nouveau nombre réel aléatoire est renvoyé chaque fois que la feuille de calcul est recalculée.»

«ALEA.ENTRE.BORNES (ALEA.ENTRE.BORNES, fonction)
Nombre aléatoire compris entre -1 et 1 (variable). Note : Lorsqu’une feuille de calcul est recalculée en entrant une formule ou des données dans une autre cellule, ou en effectuant un recalcul manuel (appuyer sur F9), un nouveau numéro aléatoire est généré pour n’importe quelle formule qui utilise la fonction ALEA. »

******************************************************************************

Donc, ce programme d’Excel, totalement déterminé mathématiquement, produit un nombre aléatoire, selon ce qui est écris.

Est-ce vrai ?

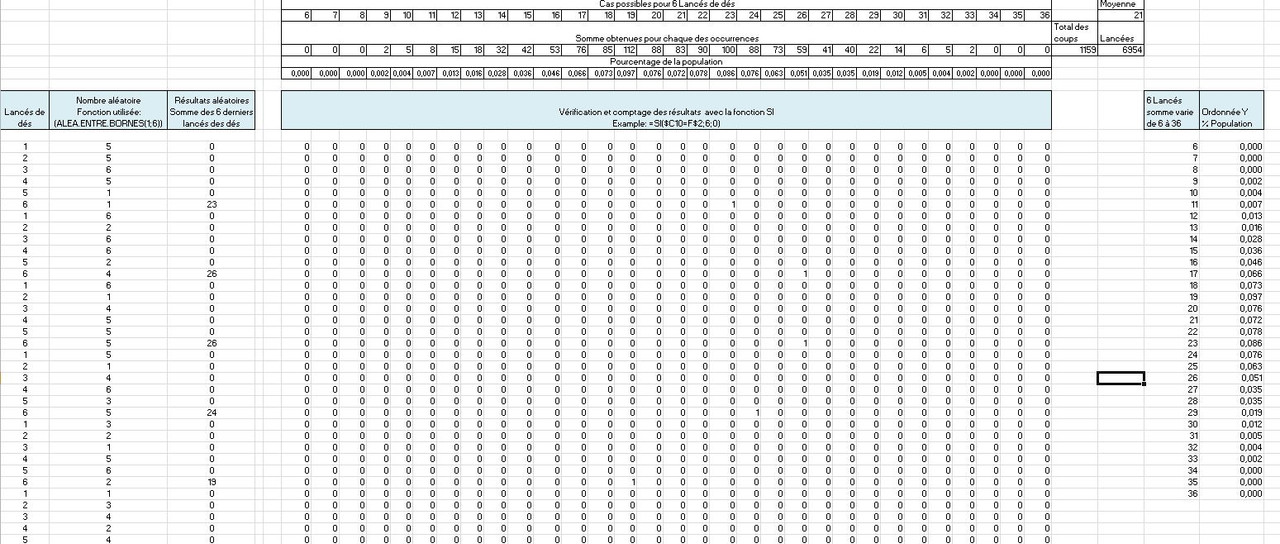
J’ai donc utilisé la fonction qui crée des nombre aléatoires de 1 à 6 (ALEA.ENTRE.BORNES(1;6)) pour simuler des lancées de dés.

La question est maintenant de prouver que ce nombre est réellement aléatoire. Pour ce faire, j’ai produit des courbes qui cumulent les résultats de plus de 6950 essais.

Pour chaque série de 6 lancés, j’ai calculé la somme et comptabilisé le nombre d’occurrences.

Si cette courbe reproduit la tendance de ce qu’on appelle la loi «normal» en probabilité/statistique, alors, on pourra en conclure que le nombre, produit de façon déterminé, est aléatoire.

***********************************************************************************************
À propos de la loi Normal, on peut se renseigner: https://fr.wikipedia.org/wiki/Loi_normale

«En théorie des probabilités et en statistique, les lois normales sont parmi les lois de probabilité les plus utilisées pour modéliser des phénomènes naturels issus de plusieurs événements aléatoires. Elles sont en lien avec de nombreux objets mathématiques dont le mouvement brownien, le bruit blanc gaussien ou d'autres lois de probabilité.

La densité de probabilité de la loi normale d'espérance μ, et d'écart type σ est donnée en équation dans la page WIKI.

*************************************************************************************************
Pour prouver le point de l’aléatoire, on peut examiner la variation des occurrences que nous obtiendrons en comparant différents résultats entre eux. Il suffit de se créer un petit programme sur une page de ce tabulateur.

J’ai utilisé les différentes capacités du programme Excel pour calculé jusqu’à 6950 cas (ou lancé de dés). En faisant la somme de six lancés, on obtiendra un résultat variant entre 6 et 36. Il faut donc ensuite comptabiliser la fréquence des répétitions et la comparer avec la Loi Normal.

Cela crée en bout de ligne un énorme tableau que l’on peut analyser plus en détail. Pour faciliter la compréhension, j’ai fait des graphiques.

Sur l’abscisse en «Y» nous avons le pourcentage d’occurrences que chaque résultat nous donne (équivalent à la somme de six lancés de dés) et sur l’abscisse «X» nous avons la somme de ces six essais ou lancés.

En comparant les divers essais, on observe que la tendance se maintient entre chaque courbes et qu’il y a une variation, donc de l’aléatoire.

Ensuite, sur une deuxième figure, je compare, la somme des résultats de plusieurs cycles d’essais, directement, avec la loi normal. Le résultat nous montre une tendance qui simule très bien cette loi Normal, prouvant ainsi la nature aléatoire de la fonction.

Attention! La série ne comprenait que 6 additions, et pour être rigoureux, j’aurais dû utiliser une somme de lancer plus élevé pour pouvoir la comparer directement avec la loi Normal des probabilités. La somme du résultat des dés pour dix lancés varieraient de 10 à 60, ce qui augmenterait la charge de calcul inutilement. C’est pour cette raison que j’ai utilisé la somme de quatre cycles d’essais avec six lancées. C’est une erreur en soi, mais, la tendance qu’on y voit est très révélatrice, ce qui est important pour notre cas.

Voici, en image, les résultats de cette «expérience» de calcul avec le tabulateur Excel.






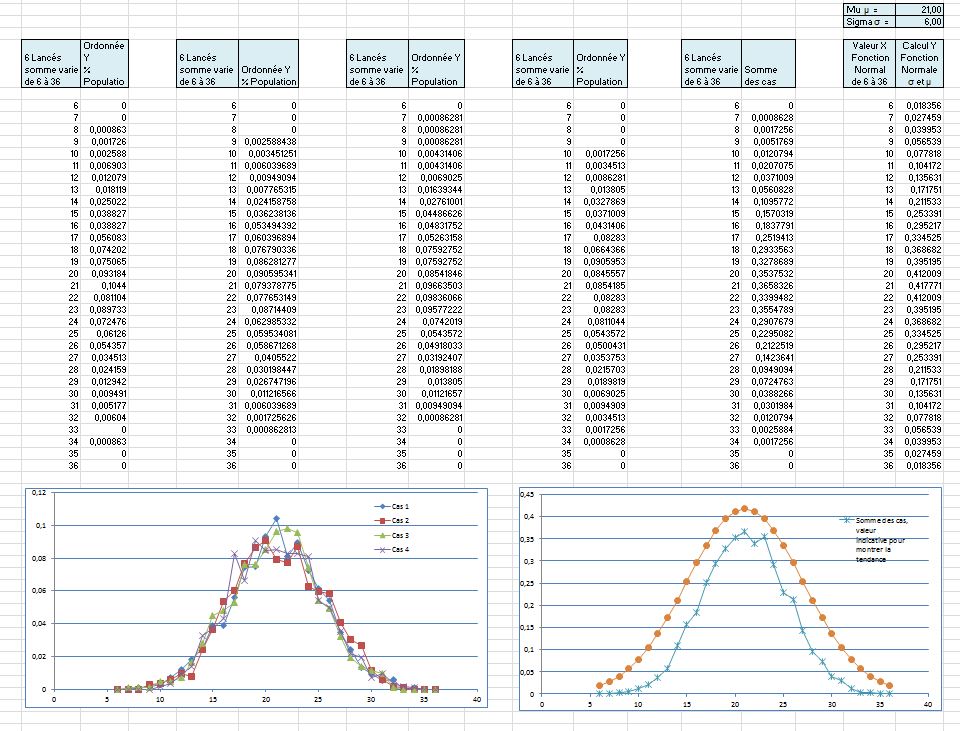
Es-tu d’accord pour dire qu’un nombre aléatoire est produit à partir de calcul mathématique déterminé ?

Etienne Beauman a écrit : 22 févr. 2021, 18:03

Dash a écrit : 22 févr. 2021, 16:47 Autrement dit, ce que nous nommons « causalité » n'est possible qu'à cause de l'imprécision qui importe en fonction de ce que l'on observe et veut reproduire, mais dans les faits, puisque rien ne se reproduit de façon parfaitement identique 2 fois de suite, ben c'est qu'il n'y a pas de causalité effective dans les faits dans l'univers Comme le suggère ABC, la causalité n'est qu'un outil!

Attention Dash, tu te fais contaminer par la propagande de Dany, le principe de causalité, c'est la cause précède l'effet, rien d'autre. et dans l'expérience du billard il est bien respecté, un joueur tape dans la boule avant qu'elle ne tombe dans le trou.
C'est le déterminisme : même cause ==> même effet qui n'est probablement qu'une illusion du à l'observateur macroscopique, quand abc parle d'expérience semblant violer le principe de causalité il parle d'expérience où de notre point de vue conditionné par la flèche du temps allant du passé vers le futur, l'effet aurait lieu avant sa cause.

Yep, j'ai juste pas utilisé le bon mot, my bad.

Dany a écrit : 22 févr. 2021, 13:12

jean7 a écrit :

Totolaristo a écrit :Mais le débat porte sur l’idée qu’on pourrait être dupé par notre pensée. Le principe c’est justement de croire qu’on est libre, de le sentir, de le tenir pour acquis.

Il est certain, là, je veux même bien qu'on parle d'évidence, que l'on est "dupé" par nos pensées et ressentit.
"Dupé" non pas que notre pensée et nos ressentis nous mentent. Simplement parce qu'ils ne peuvent pas être exacts. Ou plutôt, s'il leur arrivait de l'être sur un point précis, nous ne pourrions pas par nous mêmes identifier quoi dans ce qu'on pense est vrais.
Je ne pense pas qu'il y ait débat ou même matière à débat là-dessus.

Heu. Si, il y a débat, puisque tu affirmes (avec quelle force) que ton "libre arbitre" existe bien... rien que sur la base de tes pensées et de ton ressenti.

Tu fait cette affirmation, (avec quelle force) rien que sur la base de tes pensées et de ton ressenti.
A moins que toi tu considère ne pas être dupé, non, il n'y a pas de débat sur ce point.

Dany a écrit : 22 févr. 2021, 13:12Se méfier du langage est effectivement prudent... et bien sûr que si, nous avons la solution de ne pas faire confiance à ce langage et de chercher à redéfinir des concepts qui semblaient acquis... mais dans lesquels se cache une intention manipulatoire, qui n'a éventuellement plus de raison d'être aujourd'hui (et encore moins dans le futur avec l'avènement probable d'une cybernétique qui gommera les différences cognitives entre l'humain et les autres animaux et la machine).

Théorie du complot ?
Un des grands dangers des théories du complot, ce sont les complots qu'elles engendrent.
And so on.
Donc soit tu prouve correctement qu'il y ait eu complot. Fis un fil dessus. Les intentions manipulatoires du libre arbitres, qui, quand, comment, pourquoi. Et ça devient un fait historique partagé.
Soit tu évite de revenir là-dessus.

Dany a écrit : 22 févr. 2021, 13:12

jean7 a écrit :

Totolaristo a écrit :Vous ne pouvez pas invalider l’hypothèse sous prétexte que justement « on le sent bien qu’on est libre et que c’est nous qui décidons »

Nous ne le faisons pas !
Nous disons que les hommes sont libres parce que, dans la langue que nous partageons, il l'est.
Nous savons faire une différence entre une décision prise librement et une décision induite par des contraintes.

Ben si. Tu le fais !

Vas-y.
Affirme que les différences que nous faisons entre action contraintes et action libre dans le monde actuel n'ont aucun sens.
Mais n'oublie pas de le prouver puisque tu fais là une affirmation contraire au sens comun.

Dany a écrit : 22 févr. 2021, 13:12 Quand tu dis : "Nous disons que les hommes sont libres parce que, dans la langue que nous partageons, il l'est.", c'est de la sophistique pur jus (d'un niveau jésuitique).
...
tu es incapable de faire la différence entre une décision prise librement et un décision induite par des contraintes, mais dont tu as l'impression qu'elle est libre... simplement parce que ça confirme les concepts de ta sémantique linguistique.

Non.
Elle est libre dans le cadre usuel.
Dans ton cadre, que tu prend soins de ne pas préciser, il faudra un jour que tu prenne soin de ré-éditer un dictionnaire.

Dany a écrit : 22 févr. 2021, 13:12 Et ne me sors pas ton "si j'ai l'impression à cause du langage d'être libre, c'est que je suis vraiment libre !". Parce que, outre que c'est également hautement jésuitique, c'est aussi confondre le subjectif avec l'objectif...

Les jésuites t'obsèdent.
C'est important pour toi ?

jean7 a écrit : 23 févr. 2021, 02:36Les jésuites t'obsèdent.
C'est important pour toi ?

Une réaction emotionelle de sa part sans doute. Il serait interessant de savoir pourquoi ça l'obsède autant.

Phil_98 a écrit : 22 févr. 2021, 16:28

Totolaristo a écrit : 22 févr. 2021, 16:07 Imprévisible ne veut pas dire indéterminé...

Il faudra discuter de cette différence, qui, je pense est très importante.

Et ni l'un ni l'autre ne sont nécessaires au libre arbitre.
Aléatoire ne dit pas non plus la même chose que imprévisible ou indéterminé (prévisibilité statistique conforme à une loi).

Je ne sais pas comment Excel sort sa fonction Alea.
Mais si tu arrivais à faire entrer en interaction dans un calcul un très grand nombre de facteurs d'effets très faibles (ou très équivalents), tu obtiendrais un résultat aleatoire.

Et voilà je m’en doutais.
La fonction aléatoire de la calculatrice repose sur une formule déterminée qui utilise des paramètres changeant donnant l’illusion de l’aléatoire.

Et pour Jean, si libre arbitre = indéterminisme. C’est le principe en fait. Si vous commencez à nier dès évidence, on est pas arrivé.

Totolaristo a écrit : 23 févr. 2021, 08:30 Et pour Jean, si libre arbitre = indéterminisme. C’est le principe en fait. Si vous commencez à nier dès évidence, on est pas arrivé.

Tu veux dire que c'est ton postulat ou bien ton ressentit personel ?

Pour moi, il est évident que le libre arbitre relève du déterminisme puisqu'il se manifeste par des conséquences déterminées par des personnes.
Dire que le libre arbitre est de l'indéterminisme est donc un non sens. Si une cause précède un effet et que cette cause n'est pas reproductible, on est dans le déterminisme théorique et infalsifiable.
Le libre arbitre dit simplement que la cause peut être attribuée clairement à une personne. Ca n'interdit pas de supputer qu'il existerait des myriades de flux causaux indiscernables impliqués dans l'effet. Ils sont seulement au mieux négligeables.

Deux notions biologiques :
- l'horloge biologique interne, irréversible, plus ou moins "individualisée"
- l'oxygène, composant indispensable à la vie humaine, mais terriblement oxydatif, et précipitant le vieillissement cellulaire (cf. les radicaux libres)
Nous avons deux phénomènes, irréversibles, deux principes déterministes.
Une question :
peut-on imaginer un système fonctionnant, notamment sur le plan énergétique, indépendamment de ces conditions ?

Totolaristo a écrit :Et pour Jean, si libre arbitre = indéterminisme. C’est le principe en fait. Si vous commencez à nier dès évidence, on est pas arrivé.

Ben non, ce n'est pas le principe. Si le macroscopique recèle une part d'indéterminisme, ça invalide le déterminisme absolu de Laplace, mais ça ne veut pas dire que nous faisons des "choix" (donc ça ne veut pas dire que le libre arbitre existe autrement qu'une simple impression) :

Admettons que le monde macroscopique devienne subitement indéterministe. C'est à dire que, de manière aléatoire, les vaches se mettent soudain à voler et puis retombent par terre, que le temps se déroule parfois à rebours, que les choses changent de géométrie, que des personnes ou des choses apparaissent d'un coup devant toi, que des sensations physiques étranges surviennent et puis disparaissent, que tu te trouves dissocié ou bien, soudainement, dans un autre lieu, un autre pays, dans l'espace, suppose que tu te regardes dans la glace et que ce ne soit plus toi,... ...bref qu'il ne te soit plus possible de prévoir quoi que ce soit parce le monde devient soudain (en tout ou même en partie) fondamentalement imprédictible, donc indéterminé...

Et bien dans ce cas (si tu vis toujours), tu serais quand même contraint de réagir à tout ça... de la même manière que tu es contraint dans un monde exclusivement causal comme le nôtre.

Ces phénomènes, qui surviendraient aléatoirement, t'obligeraient à t'adapter à ce nouveau monde et tu le ferais sous la contrainte de tes déterminants antérieurs.

Que notre univers macroscopique de tous les jours, soit régit exclusivement par le principe de causalité ou qu'il recèle des phénomènes aléatoires ne change rien au fait que nous sommes toujours contraints par l'environnement et par nos déterminants antérieurs.

Sinon, jean7 semble à première vue dire la même chose que moi sur ce sujet (mais en fait pas vraiment. En plus, il devient parfaitement incompréhensible... indéterminé)

@Dany

Si le libre arbitre existe, il s’agit forcément d’indéterminisme. Mais si l’indéterminisme existe, ça n’implique pas nécessairement le libre arbitre.
Je maintiens et je signe.

Totolaristo a écrit :Si le libre arbitre existe, il s’agit forcément d’indéterminisme. Mais si l’indéterminisme existe, ça n’implique pas nécessairement le libre arbitre.
Je maintiens et je signe.

Ah, ok. J'avais mal saisi ton post :

Totolaristo a écrit :Et pour Jean, si libre arbitre = indéterminisme. C’est le principe en fait. Si vous commencez à nier dès évidence, on est pas arrivé.

C'est mon avis aussi (d'où mon post au dessus). Il me semble d'ailleurs qu'une majorité des intervenants est d'accord là dessus. (enfin tu vas trouver que je chipote, mais dès lors, il n'est pas juste d'écrire "libre arbitre = indéterminisme". Ca prête à confusion comme formulation, parce que "indéterminisme -> libre arbitre" n'est pas vrai)

DictionnairErroné a écrit : 22 févr. 2021, 14:20 La volonté, l'attention, la délibération, la décision sont les marques du libre arbitre de la pensée.

Quel est le processus?

• L'attention se dirige vers une situation.

• La volonté entretien une délibération.

• Il y a conclusion, le fiat*, la décision.

Qu'avons-nous ici? Une cause (l'attention) et l'effet (le fiat). Une chaîne causale du modèle déterministe. L'entre-deux est-il libre? Que se passe-t-il à partir de la cause pour arriver à l'effet dans la pensée? Peut-il exister un libre arbitre dans le processus déterministe de la pensée?

Réflexion à suivre


*Décision volontaire mettant fin à une délibération

Reformulons la question: Peut-il exister une non prévisibilité dans le processus déterministe de la pensée?

À partir de la cause à l'effet de la pensée peut-il exister une transition non prédictive, non prévisible? La contingence* pourrait-elle être cette transition qui donne l'impression du libre arbitre de la pensée.

*le fait d'une chose peut ou non se produire

Dico a écrit :Reformulons la question: Peut-il exister une non prévisibilité dans le processus déterministe de la pensée?

Forcément et il y en a plein. De l'imprédictible (et non nécessairement de l'indéterminisme qui serait fondamental), il n'y a pratiquement que ça dans le processus de la pensée, qui est d'ailleurs en majeure partie inconsciente et donc indiscernable au point de vue subjectif.

Déjà, Tu as l'air de croire que ce que tu appelles, la volonté, l'attention, la délibération, la décision,... sont des processus de pensée forcément conscients. C'est faux, on n'en voit que la partie émergée de l'iceberg.
Mais que cette petite partie qu'on nomme le "conscient" nous donne l'impression de choisir, ça ne m'étonne pas du tout, surtout si le langage participe au renforcement de cette sensation et qu'on ne remet jamais en doute son rôle dans l'affaire...

Dany a écrit : 23 févr. 2021, 16:52

Totolaristo a écrit :Si le libre arbitre existe, il s’agit forcément d’indéterminisme. Mais si l’indéterminisme existe, ça n’implique pas nécessairement le libre arbitre.
Je maintiens et je signe.

Ah, ok. J'avais mal saisi ton post :

Totolaristo a écrit :Et pour Jean, si libre arbitre = indéterminisme. C’est le principe en fait. Si vous commencez à nier dès évidence, on est pas arrivé.

C'est mon avis aussi (d'où mon post au dessus). Il me semble d'ailleurs qu'une majorité des intervenants est d'accord là dessus. (enfin tu vas trouver que je chipote, mais dès lors, il n'est pas juste d'écrire "libre arbitre = indéterminisme". Ca prête à confusion comme formulation, parce que "indéterminisme -> libre arbitre" n'est pas vrai)

C’est un peu du chipotage effectivement (selon moi).
La poule est un oiseau mais tous les oiseaux ne sont pas des poules.
Plutôt que de dire Poule = oiseau, je devrais dire la poule appartient au groupe Oiseau.

Pour Phil le libre arbitre pourrait être issu du déterminisme. Pour moi c’est un non sens que j’ai déjà expliqué.
Phil persiste dans cette vision avec l’exemple de la fonction « aléatoire ». Qui prouve selon moi qu’on en est clairement pas tous au même niveau dans nos réflexions...

Dany a écrit : 23 févr. 2021, 17:40 Déjà, Tu as l'air de croire que ce que tu appelles, la volonté, l'attention, la délibération, la décision,... sont des processus de pensée forcément conscients. C'est faux, on n'en voit que la partie émergée de l'iceberg.

Wo, wo, wo, là! Vous croyez que ce processus (attention, volonté, délibération, décision) est principalement inconscient?

Dany a écrit : 23 févr. 2021, 17:40 Mais que cette petite partie qu'on nomme le "conscient" nous donne l'impression de choisir, ça ne m'étonne pas du tout, surtout si le langage participe au renforcement de cette sensation et qu'on ne remet jamais en doute son rôle dans l'affaire...

Je distingue la conscience du conscient. La conscience est comme un lieu nu, un état. C'est dans ce lieu que sont les pensées, les émotions, les délibérations, etc. Je ne sais pas comment l'exprimer autrement que par un lieu. Comme je disais ailleurs, je réfère à cette sensation lorsque nous arrêtons le dialogue intérieur par exemple. Cet état existe même si nous arrêtons de penser, etc., la conscience.

Pourquoi fais-je cette distinction? C'est que nous n'avons aucune idée qu'est cet "état", ce "lieu" ou "émergence", qui sait! Alors c'est un inconnu dans la connaissance de la pensée. Il m'apparaît que le déterminisme s'applique au processus de la pensée (attention, volonté, délibération, décision) mais est-ce suffisant pour comprendre ce qui s'y passe?

@Dico

Je pense que ça ne serait pas étonnant d’apprendre que la majorité des processus aboutissant à une pensée soient inconscients. En tout cas ça ne me choquerait pas plus que ça.


Si l’hypothèse du non libre arbitre et du cerveau déterminé sont vraies, on pourrait entièrement « fabriquer » une conscience qui serait comparable à la notre.

Dico a écrit :

Dany a écrit :Déjà, Tu as l'air de croire que ce que tu appelles, la volonté, l'attention, la délibération, la décision,... sont des processus de pensée forcément conscients. C'est faux, on n'en voit que la partie émergée de l'iceberg.

Wo, wo, wo, là! Vous croyez que ce processus (attention, volonté, délibération, décision) est principalement inconscient?

Bien sûr.
La conscience est alimentée, modifiée, altéré, par l'ensemble des traitements cognitifs inconscients. Les aires principales du conscient sont situées dans l'hémisphère du langage (on pense d'ailleurs que la conscience supérieure est intimement liée au langage), ce sont la région du cortex frontal gauche et la région corticale postérieure gauche. Mais plusieurs autres régions s'allument à l'IRM dans une prise de décision ou bien un mouvement dit "volontaire" quelconque.

Wikipedia a écrit :L'étude de la conscience met en évidence un fait remarquable : la plupart des processus du système nerveux sont inconscients (au sens cognitif). ...

...Le cerveau de patients ayant une héminégligence traite cependant l'information visuelle présentée dans le champ « négligé ». Après lésion du cortex visuel, le cerveau reste capable de localiser inconsciemment des objets dans le champ visuel (phénomène de la « vision aveugle »). ...

...Dans la pathologie appelée prosopagnosie, la reconnaissance consciente d'un visage est impossible, mais les réactions physiologiques indiquent que le visage vu est inconsciemment reconnu. Certaines données montrent qu'apparemment le traitement du stimulus perçu emprunte le même chemin, que la perception soit « consciente » ou « inconsciente ».

...Ainsi la tomographie à émission de positons met en évidence qu'en l'absence de toute focalisation particulière de l'attention, l'activité du cerveau (activité intrinsèque du réseau du mode par défaut, nommée « énergie sombre du cerveau » par analogie à l'énergie sombre du cosmos et qui consiste en des vagues d'ondes électriques lentes) correspond à une dépense de 60 à 80 % de toute l'énergie consommée par le cerveau, soit une énergie 20 fois supérieure à celle consommée par le cerveau lorsqu'il réagit consciemment, la réalisation d'une tâche particulière (activité consciente moins fréquente que l'activité inconsciente) exige une énergie qui n'excède pas 5 % de celle consommée par l'activité de fond

Voir aussi l'inconscient cognitif.

Dico a écrit :Je distingue la conscience du conscient. La conscience est comme un lieu nu, un état. C'est dans ce lieu que sont les pensées, les émotions, les délibérations, etc. Je ne sais pas comment l'exprimer autrement que par un lieu. Comme je disais ailleurs, je réfère à cette sensation lorsque nous arrêtons le dialogue intérieur par exemple. Cet état existe même si nous arrêtons de penser, etc., la conscience.

C'est une élucubration qui t'es personnelle. Pourquoi pas...
Il me semble plutôt que quand on arrive à arrêter notre dialogue intérieur (ce qui est bien plus facile à dire qu'à faire), on entre dans un état de méditation... qui montre justement une image IRM très différente de celle d'un état de conscience courant.
Sinon "la conscience" ou "le conscient", c'est synonyme...

Dany a écrit : 24 févr. 2021, 00:43 C'est une élucubration qui t'es personnelle. Pourquoi pas...
Il me semble plutôt que quand on arrive à arrêter notre dialogue intérieur (ce qui est bien plus facile à dire qu'à faire), on entre dans un état de méditation... qui montre justement une image IRM très différente de celle d'un état de conscience courant.
Sinon "la conscience" ou "le conscient", c'est synonyme...

Reprenons, cesser la délibération intérieure complètement, fermer vos yeux, etc. Ce qui reste, ce que nous expérimentons est ce que j'appelle la conscience. Dans la conscience apparait la pensée, les émotions, les sentiments, etc. Pour moi la distinction est importante car elle donne du sens à ce que j'expérimente.

Que je sois dans un état normal, drogué, saoul, c'est ce qui est conscient qui change, la conscience elle-même est toujours présente inchangé. La conscience disparaît dans certain stage du sommeil, le black-out! Donc un état relier à une certaine activité cérébrale ou autre patente dans le cerveau. Mais quoi? C'est un inconnu qui me titille et ne me permet pas de me prononcer sur l'existence ou non du libre arbitre.

Dany a écrit : 24 févr. 2021, 00:43

Dico a écrit : Wo, wo, wo, là! Vous croyez que ce processus (attention, volonté, délibération, décision) est principalement inconscient?

Bien sûr.

Wikipedia
l'inconscient cognitif

De ce point vu, oui, presque la totalité de l'activité cérébrale n'est pas consciente, je préfère ne pas utiliser le mot inconscient parce que j'en ai pas terminé avec lui.

Si vous me permettez, j'ai le goût de vous bavez un peu, vous m'en donnez le goût vous, vous pouvez sauter le divulgâcheur si vous voulez.

Totolaristo a écrit : 23 févr. 2021, 14:07 @Dany
Si le libre arbitre existe, il s’agit forcément d’indéterminisme.

Même en applicant tes conceptions théoriques du libre arbitre, du choix, etc., qui tournent le dos à certains faits, et pour poursuivre sur du chipotage (donc j'accepte un chipotage pour en produire un autre en quelque sorte), l'indéterminisme dont tu parle ici n'est indéterminisme que vis-à-vis du déterminisme de Laplace.

jean7 a écrit : 24 févr. 2021, 02:54

Totolaristo a écrit : 23 févr. 2021, 14:07 @Dany
Si le libre arbitre existe, il s’agit forcément d’indéterminisme.

Même en applicant tes conceptions théoriques du libre arbitre, du choix, etc., qui tournent le dos à certains faits, et pour poursuivre sur du chipotage (donc j'accepte un chipotage pour en produire un autre en quelque sorte), l'indéterminisme dont tu parle ici n'est indéterminisme que vis-à-vis du déterminisme de Laplace.

Non. Vis à vis du déterminisme de manière général.

Totolaristo a écrit : 24 févr. 2021, 07:53 Non. Vis à vis du déterminisme de manière général.

celui-là ? :
"Le déterminisme est une notion philosophique selon laquelle la succession de chaque événement est déterminée en vertu du principe de causalité, du passé et des lois de la physique."

pourquoi ?

Dany à DicoE a écrit : 24 févr. 2021, 00:43 Tu as l'air de croire que ce que tu appelles, la volonté, l'attention, la délibération, la décision,... sont des processus de pensée forcément conscients. C'est faux, on n'en voit que la partie émergée de l'iceberg.
Mais que cette petite partie qu'on nomme le "conscient" nous donne l'impression de choisir, ça ne m'étonne pas du tout
...
Il me semble plutôt que quand on arrive à arrêter notre dialogue intérieur (ce qui est bien plus facile à dire qu'à faire), on entre dans un état de méditation... qui montre justement une image IRM très différente de celle d'un état de conscience courant.

C'est justement ça qui me pose question. Pour entrer en méditation, il faut faire un effort de conscience sur l'inconscient. C'est la conscience qui prend les rênes à ce moment pour faire taire l'inconscient et le "modeler" temporairement à la méditation.

Alors qu'il y ait des décisions inconscientes, bien sur, mais la décision consciente existe bien pour entrer en méditation par ex.

Quant à la volonté, je pense qu'elle est uniquement consciente. Dans l'insconscient il ne peut pas y avoir de place pour la volonté puisque c'est simplement le déroulement d' un enchainement logique de déterminants qui se succèdent jusqu'au résultat final.

Dans ma bulle imaginaire pourrions-nous dire que le déterminisme est le libre arbitre? Il y aurait délibération* entre les éléments en cause pour aboutir à une décision, l'effet? N'est-ce pas ce qui se passe dans la conscience?


*par exemple, différentes lois physiques, thermiques, quantiques... se frottent les unes les autres, chacun ayant sa valeur propre.