Forum Sceptique

Ma question est pas mal hors sujet vis-à-vis le thème global du forum, mais j'ai décidé de poster sur cette section compte tenu de sa description "Ici, on discute de sujets variés...". M'enfin qu'un administrateur ne se gène pas à déplacer le fil ailleurs.

Bon, moi et mes copains gamers somme sous l'emprise du jeu de carte "Dominion". À la dernière soirée, nous avons débattu sur une question de probabilité, mais nos connaissances en la matière nous a fait défaut, et n'avons pas pût trouvé la réponse à notre question.

Voilà le problème posé sans tomber dans les détails du jeu.

1) On a un paquet de 10 cartes, soit exactement 7 cartes "A" et 3 cartes "B".

2) On mélange le paquet à l'aveuglette.

3) On divise, toujours à l'aveuglette, le paquet en deux, soit deux piles de 5 cartes chacune.

Question: Quel est le % de chance pour que les 3 cartes "B" se retrouvent dans la même pile?

Merci !!!!

Salut Chiwaw,

Chiwaw a écrit : Question: Quel est le % de chance pour que les 3 cartes "B" se retrouvent dans la même pile?

Je dirais 1 chance sur 6... (4/9 * 3/8 = 1/6).

Hallu

Je dirais 1 chance sur 36: (5! x 7!) / (3! x 10!)

J'ai changé d'idée moi aussi.

Dans le tableau qui suit, j'ai nommé les trois cartes "B": 1,2 et 3.

Les répartitions possibles sont:

PILE #1.....PILE #2
-----------------------
1,2,3 ......... 0
1,2 ........... 3
1,3 ........... 2
2,3 ........... 1
1 .............. 2,3
2 .............. 1,3
3 .............. 1,2
0 .............. 1,2,3

Donc la probabilité de retrouver les cartes 1,2 et 3 dans une des deux piles est de 2 sur 8, soit 1 chance sur 4.

P.S. Excusez les multiples éditions. J'ai eu de la difficulté à aligner mon tableau.

Ouais je dirais comme Hallu finalement

Au pif, je dirais une chance sur 4.

Je me dis que chaque carte a une chance sur 2 de se retrouver dans une pile donnée.

Le première carte B distribuée va dans une pile à coup sûr. La probabilité que les 2 autres cartes B soient tirées dans la même pile serait donc de 1/2^2 = 1/4.

Ça me semble logique à première vue, mais je me méfie de ma logique des probabilités. J'ai bien hâte d'avoir la réponse d'un pro (à la Denis).

Amicalement,
Phil

Salut Chiwaw,

Comme Hallu et Zwielicht, j'arrive à 1 chance sur 6.

Ton problème se résout via la Loi Hypergéométrique.

Le nombre X de cartes de type B dans la pile # 1 suit une loi hypergéométrique avec N=10, n=5 et m=3.

En utilisant la formule donnant les probabilités de chaque valeur possible pour X,



on trouve :

P(X=0) = 1x21/252 = 1/12
P(X=1) = 3x35/252 = 5/12
P(X=2) = 3x35/252 = 5/12
P(X=3) = 1x21/252 = 1/12
--- Total --- = 12/12 = 100%

La probabilité que les 3 cartes B soient dans la même pile est

P(X=0) + P(X=3) = 2/12 = 1/6.

Denis

Je fais équipe avec Philippe.

On est deux à dire que la probabilité est de 1 sur 4.

Vous êtes trois à dire qu'elle est de 1 sur 6.

Qui va gagner: l'équipe des zozos ou celle des zézés ?

Salut Raphy,

Tu dis :

PILE #1.....PILE #2
-----------------------
1,2,3 ......... 0
1,2 ........... 3
1,3 ........... 2
2,3 ........... 1
1 .............. 2,3
2 .............. 1,3
3 .............. 1,2
0 .............. 1,2,3

Donc la probabilité de retrouver les cartes 1,2 et 3 dans une des deux piles est de 2 sur 8, soit 1 chance sur 4.

Ta solution serait correcte si tes 8 cas étaient équiprobables.

Or, ils ne le sont pas. Je trouve que les probabilités de chacun de tes 8 cas sont :

PILE #1.....PILE #2
-----------------------
1,2,3 ........ 0 ...............Prob = 3/36
1,2 ........... 3 ...............Prob = 5/36
1,3 ........... 2 ...............Prob = 5/36
2,3 ........... 1 ...............Prob = 5/36
1 .............. 2,3 ............Prob = 5/36
2 .............. 1,3 ............Prob = 5/36
3 .............. 1,2 ............Prob = 5/36
0 .............. 1,2,3 .........Prob = 3/36

La probabilité que les cartes 1,2,3 soient dans la même pile est donc 3/36 + 3/36 = 1/6.

Denis

J'essaie de faire le parallèle entre mon résultat, celui de Raphaël (après édition) et celui de Denis.

Je crois que la "logique" de ma réponse est bien démontrée dans le tableau de Raphaël. En voyant la formule utilisée par Denis, je comprends que la variable N (10 cartes) a une importance que nous avons négligé.

Je comprend la formule, mais d'un point de vu pratiquo~pratique, je ne visualise pas la différence entre un paquet de 10 et de 20 cartes dans la répartition des 3 qui nous intéressent. Mystère à régler, toute aide est la bienvenue.

Amicalement,
Phil

Edit : Raphaël, désolé d'être si peu solidaire, mais je n'ai pas le profil zozo nécessaire pour être membre de ton équipe. Denis a souvent dit "on ne se bat pas contre un théorème", moi je dis "dans un problème de probabilités, on ne se bat pas contre Denis".

Denis a écrit :Ta solution serait correcte si tes 8 cas étaient équiprobables.

Or, ils ne le sont pas. Je trouve que les probabilités de chacun de tes 8 cas sont :

PILE #1.....PILE #2
-----------------------
1,2,3 ........ 0 ...............Prob = 3/36
1,2 ........... 3 ...............Prob = 5/36

Pourquoi la carte #3 aurait plus de chance de se retrouver dans la deuxième pile que dans la première ?

Serait-ce un caprice de sa part ?

Explique-moi S.T.P.

Salut Phil,

Tu dis :

Je comprend la formule, mais d'un point de vu pratiquo~pratique, je ne visualise pas la différence entre un paquet de 10 et de 20 cartes dans la répartition des 3 qui nous intéressent. Mystère à régler, toute aide est la bienvenue.

Je vais essayer de te le faire voir en comparant deux cas extrêmes.

(a) Quand on a 1 zillion de cartes (dont 3 cartes 1,2,3) qu'on partage en 2 piles de ½ zillion de cartes chacune.

(b) Quand on a 6 cartes (dont 3 cartes 1,2,3) qu'on partage en 2 piles de 3 cartes chacune.

Dans le cas (a), les 8 cas listés par Raphy sont équiprobables et la réponse est votre 1/4.

Quand il y a "une infinité" de cartes, la carte 2 a une chance sur 2 d'être dans la même pile que la carte 1. Puis la carte 3 a une chance sur 2 d'être dans la pile où il y a les cartes 1 et 2. En fin de compte, ½ x ½ = ¼.

Dans le cas (b) où on n'a que 6 cartes, on a 2 chances sur 5 que la carte #2 soit placée dans un des 2 "espaces libres" de la pile où on a placé la carte 1. Puis on a 1 chance sur 4 que la carte #3 soit placée dans le seul espace libre restant (dans la pile où on a déjà placé 1 et 2) plutôt que dans un des 3 espaces libres de l'autre pile. En fin de compte, (2/5)x(1/4) = 1/10.

Le cas de Chiwaw (avec 10 cartes) est intermédiaire entre les cas (a) et (b). La réponse (1/6) est intermédiaire entre les deux autres réponses (1/4 et 1/10).

Si on a 20 cartes (partagées en 2 piles de 10), la réponse est (9/19)x(8/18) = 4/19.

Si on a 2n cartes (avec n ≥ 3), la réponse générale est ((n-1)(n-2))/((2n-1)(2n-2)).

Tu dis aussi :

Denis a souvent dit "on ne se bat pas contre un théorème", moi je dis "dans un problème de probabilités, on ne se bat pas contre Denis".

Ça dépend du problème.

J'ai déjà dit, sur le forum, que si on mettait bout-à-bout toutes les fautes de calcul que j'ai faites durant ma vie, ça ferait environ 13.5 fois le tour de la Terre.

Ici, tu dis :

Depuis un bon bout de temps, je suis plutôt inactif sur le forum, c'est surtout une question de temps...

Prends ta retraite. Ça règlera ce problème.

...au risque d'en créer d'autres.

Denis

Salut Raphy,

Tu dis :

Pourquoi la carte #3 aurait plus de chance de se retrouver dans la deuxième pile que dans la première ?

Serait-ce un caprice de sa part ?

Explique-moi S.T.P.

Partager 10 cartes (dont trois marquées 1,2,3) en deux piles, c'est comme les partager en deux lignes de 5 espaces.

Supposons qu'on a déjà placé les cartes 1 et 2 et qu'elles sont dans la même ligne. On a une disposition qui ressemble à ça :



En plaçant la carte #3 au hasard dans une des 8 cases libres, on a 5 chances sur 8 de la placer dans la ligne vide et 3 chances sur 8 de la placer dans la ligne où sont déjà placées les cartes 1 et 2.

J'espère que c'est plus clair qu'avant.

Denis

Salut Denis,

Merci pour ces explications. Comme d'habitude, t'as mis le doigt directement sur le bobo. Toujours un plaisir de te lire.

Je comprends pourquoi t'as choisi de faire carrière dans l'enseignement des maths. Une fois un problème bien solutionné, c'est case closed, il n'y a plus de doutes. Ça fait différent des problèmes existentiels en teintes de gris.

Dans un autre ordre d'idées, tu dis

Denis a écrit : Prends ta retraite. Ça règlera ce problème.

Je le ferai quand j'en aurai le temps. D'ici 40 ans, promis.

Amicalement,
Phil

Salut,

Denis a écrit :

C'est comme ça que je suis arrivé au résultat.

On a 3 cartes B1, B2 et B3.

Probabilité que la carte B1 se retrouve dans l'un des deux tas : 100%.
Probabilité que la carte B2 se retrouve dans le même tas que la carte B1 : 4 chances sur 9 (il reste neuf places possibles, dont 4 dans le tas qui contient B1).
Probabilité que la carte B3 se retrouve dans le même tas que les deux autres : 3 chances sur 8 (il reste huit places possibles, dont 3 dans le tas qui contient B1 et B2).

Donc probabilité totale d'avoir B1, B2 et B3 dans le même tas = 4/9 * 3/8 = 1/6

Amicalement,
Hallucigenia

Salut,
une autre manière de voir, accessible à partir d'un cours de Terminale (il me semble)
1. je choisi 3 nombres parmi 10, il y a C103 combinaisons possibles.
C103 = 120
2. Parmi toutes ces combinaisons, je repère celles où je choisis mes 3 nombres parmi les 5 premiers nombres, il y en a C53 = 10.
3. Parmi toutes ces combinaisons, je repère celles où je choisis mes 3 nombres parmi les 5 derniers nombres, il y en a C53 = 10.

Les cas 2 et 3 sont ceux où les 3 cartes sont toutes dans un seul demi-paquet.

donc probabilité totale d'avoir les 3 cartes dans un seul demi-paquet = 2 x C53 / C103 = (2x10)/120 = 1/6

Il me semble que c'est une application de la loi donnée par Denis plus qu'autre chose.

Merci à tous! Et un merci spécial à Denis car avec son petit graphique:

Denis a écrit :

j'ai réalisé que j'aurais sans doute été capable d'en venir à la même conclusion si j'avais pris la peine justement de visualiser le problème sur papier plutôt que d'essayer de me souvenir de formules abstraites oubliés il y a belle lurette.

Pourquoi faire compliqué quand on peux faire simple?

Et 1/6 semble justement très proche de ce que j'ai remarqué comme distribution lors de mes observations du jeu.

Salut à tous ceux qui ont participé à cette enfilade.

Dans le temps où j'en avais, je disais souvent à mes étudiants que résoudre un problème d'analyse combinatoire (le problème de Chiwaw en est un) c'est un peu comme défaire un noeud de ficelle. On peut faire glisser une boucle avant ou après une autre : en fin de compte, ça revient au même.

Il y a souvent plusieurs solutions équivalentes (i.e. plusieurs façons correctes d'arriver à la réponse correcte). La meilleure solution n'est pas nécessairement la plus simple, ni la plus courte. C'est plutôt celle où l'on voit le mieux qu'on ne se trompe pas.

Je pense que, parmi toutes les réponses correctes qu'on a trouvées, la plus simple est probablement celle de Hallu (qui est probablement aussi celle de Zwielicht). Celle de Ptoufle la chauffe de près. J'admets que ma première solution (via la loi hypergéométrique) était "inutilement forte". Un peu comme sortir la grosse souffleuse pour déblayer 1 cm de neige.

La solution de Raphy était peut-être encore plus simple que celle de Hallu, mais elle avait le gros défaut d'être incorrecte.

Le problème de Chiwaw peut être généralisé en remplaçant son 3 et son 5 par k et n.

On a 2n cartes, parmi lesquelles k sont de type B et (2n-k) sont de type A (avec k ≤ n). On brasse ces cartes et on en fait deux piles de n cartes chacune.

La probabilité que les k cartes de type B soient dans la même pile est alors :



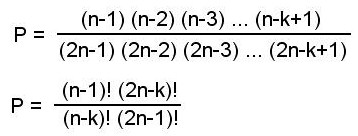
Ces deux formules, algébriquement équivalentes, s'obtiennent à la fois par la méthode de Hallu, par la méthode de Ptoufle et par la grosse souffleuse hypergéométrique.

Avec n=5 et k=3 (le cas de Chiwaw), elles donnent P = 1/6.

Avec, par exemple, n=26 et k=13 (13 cartes de coeur parmi 52 cartes), elles donnent P = 0.000032757.

Quand on partage au hasard un jeu de 52 cartes en deux piles de 26, on a donc environ une chance sur 30528 que les 13 cartes de coeur se trouvent dans la même pile.

Denis

P.S. À moins, évidemment, que je me sois trompé dans mes calculs, ce qui n'est pas absolument absolument absolument impossible.

Salut Denis,

Denis a écrit : Je pense que, parmi toutes les réponses correctes qu'on a trouvées, la plus simple est probablement celle de Hallu

Et je suis aussi le premier à avoir répondu.

Qu'est-ce que j'ai gagné ?

Hallu

Salut Hallu,

Tu dis :

Qu'est-ce que j'ai gagné ?

En effet, ça mérite un prix.

Je t'offre le choix entre un point zézé et un bec sucré de qui tu voudras.

Denis

Denis a écrit : En effet, ça mérite un prix.

Chouette ! J'aurais volontiers opté pour le baiser, mais je ne souhaite imposer à personne de me le donner.

J'accepte donc fièrement cette médaille virtuelle. Merci !

Hallu

Bon allez, pour rester dans l'esprit du fil (et de la raison initiale de ma question), je te récompense donc avec une carte de Copper (carte A) et une carte d'Estate (carte B).



Fais-en bon usage!

Denis a écrit :En plaçant la carte #3 au hasard dans une des 8 cases libres, on a 5 chances sur 8 de la placer dans la ligne vide et 3 chances sur 8 de la placer dans la ligne où sont déjà placées les cartes 1 et 2.

J'espère que c'est plus clair qu'avant.

Oui, c'est très clair.

Merci de m'avoir détordu.