Problème de probabilité élémentaire

[PhilippeL]

Bonjour à tous,

Bien qu'il m'arrive de vous lire, ma dernière intervention sur le forum date un peu alors je commence par vous souhaiter la bonne année à tous!

Je surfais tardivement et je lisais la version ebook du livre de Normand Baillargeon : Petit cours d'autodéfense intellectuelle. Je suis tombé sur le problème de dés du Chevalier de Méré et de Blaise Pascal, disponible vers la moitié de cette page. C'est là que je me rend compte que je raisonne comme ce pauvre Chevalier de Méré qui s'est fait faire la leçon il y a quelques siècles de cela... dur constat. J'aurais besoin d'explications précises pour mettre le doigt directement sur le bobo. Analysons la première partie du problème, c'est tout ce qui m'intéresse, le reste en découle :

Quelle est la probabilité d'obtenir au moins un 6 en tirant 4 fois un dé à 6 faces bien balancé?

La réponse du Chevalier de Méré (tout comme mon raisonnement instinctif) est : la probabilité de tirer un 6 est de 1/6 donc si j'ai 4 tirs, la probabilité est de 1/6 * 4 = ~67%.

La "bonne" réponse, donnée par Blaise Pascal est pourtant : 1 - (5^4 / 6^4) = ~52%.

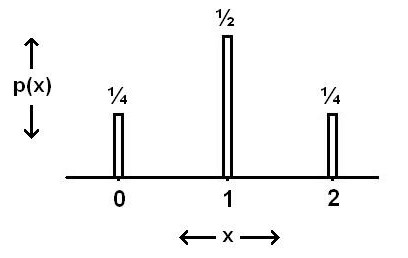
Je croyais bien qu'il existait une quelconque loi qui permettait d'additionner les probabilités lorsqu'il y a plusieurs "tirs" indépendants. Par exemple, si on me demande la probabilité de tirer au moins une fois "pile" avec un 25 cents avec 2 essaies, je dirais qu'elle est de 1, soit 1/2 *2.

Pour cerner encore plus ma zone d'incompréhension, j'ai du mal à comprendre la formule de Pascal : 1 - (5^4 / 6^4). Pour 6 tirs (en remplaçant les exposants 4 pour 6), j'arrive à 66.5% (alors que dans ma tête, ça devrait arriver à 1). La formule ressemble donc à une sorte de série qui tend vers 1 et pourtant, si je lance le dé > 6 fois, je me dis toujours que je devrais statistiquement obtenir > un 6.


À mesure que j'écris ces lignes, je me démêle moi-même et me rend compte que ces 2 valeurs ont des interprétations différentes . En effet, comment la chance d'obtenir au moins un 6 pourrait être plus grande que 100% ? Par contre, pour revenir au problème du Chevalier de Méré, pourquoi ces valeurs sont différentes et pourquoi est-ce que le calcul de Blaise Pascal est celui à utiliser pour calculer les probabilités de gagner du Chevalier de Méré? [/pensées de mon cerveau] je sais j'ai pas ouvert la balise


Pour terminer, je copie cet extrait d'une explication sommaire des problèmes et calcul (notons que je m'intéresse pour l'instant qu'au 1) que j'ai trouvé sur un site anglophone :

Chevalier de Mere's Problem

Compare two problems:

1. What is the probability of having at least one 1 in four rolls of a dice?

2. What is the probability of having at least one double 1 in 24 rolls of two die?

Solution to Problem 1

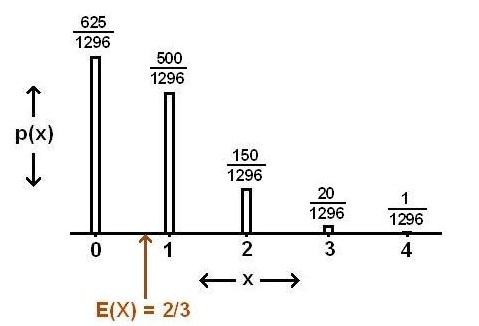
Four rolls of a dice may have one of 6^4 equiprobable outcomes. Of these, 5 4 are unfavorable leaving (6^4 - 5^4) favorable for the bet. The probability of getting at least 1 ace is then

(6^4 - 5^4) / 6^4 = (1296 - 625) / 1296
= 671 / 1296
≈ 0.5177 ...
> 0.5

showing that the odds are in favor of the bettor.
Solution to Problem 2

One double roll has 36 equiprobable out comes of which 35 are unfavorable to the bet. In 24 rolls there are 3624 possible outcomes of which only (36^24 - 35^24) are favorable. Thus the probability of winning the bet equals

(36^24 - 35^24) / 36^24 = 1 - (35/36)24
≈ 1 - 0.5086
= 0.4914
< 0.5.

Merci de m'aider à comprendre totalement ces concepts et ainsi de pouvoir jouir à nouveau de la vie.

Amicalement,
Phil

[PARKONTEL]

Une probabilité est un nombre réel variant de 0 à 1, plus elle est grande plus l'évènement a de chance de se produire. Une proba de 1 indique que l'évènement va se produire.
Tu dis :
"Par exemple, si on me demande la probabilité de tirer au moins une fois "pile" avec un 25 cents avec 2 essaies, je dirais qu'elle est de 1, soit 1/2 *2."

Penses-tu que chaque fois que tu lances 2 fois de suite une pièce alors tu obtiendras toujours au moins une fois pile ?
La notion d'indépendance des évènement entre ici en jeu : ce n'est pas parceque tu as obtenu un face à ton premier jet de pièce que tu vas forcément obtenir un pile au second. Le résultat d'un lancer n'influe pas sur le résultat du prochain lancer.
Théoriquement tu peux être très mal chanceux et faire 100 jets "face" à la suite.

Pour ton jet de dés la proba d'obtenir un 6 sur un jet est de 1/6 (sur le second jet elle est aussi de 1/6). Notons cette proba P(A).
La probabilité de l'évènement contraire "ne pas obtenir de 6" est de 5/6 à chaque jet. Notons cette proba P(non A).
La probabilité que "j'obtienne un 6 ou que je n'obtienne pas de 6 sur un lancer" est sur de se produire et est donc de 1. P(A) + P(non A) = 1
Tu obtiens : P(A)=1 - P(non A)

La formule pour calculer le fait d'obtenir au moins un 6 sur 4 lancers est alors :
P(A)=1 - (5/6)^4 avec P(non A) = (5/6)x(5/6)x(5/6)x(5/6)

En fait tu biaises en te disant que la proba d'obtenir un 6 est 1/6 pour un lancer, donc de (1/6)*4 pour 4 lancers. Il faudrait que tu te dises que c'est la proba de faire un 6 plus la proba de faire deux 6, plus la proba de faire trois 6 etc ... il y a la notion de "au moins" qui est importante.

[PhilippeL]

Salut PARKONTEL,

Merci d'essayer de m'aider à m'éclairer.

Penses-tu que chaque fois que tu lances 2 fois de suite une pièce alors tu obtiendras toujours au moins une fois pile ?

Effectivement, non. Je pense par contre que si j'étais un joueur de pile ou face (contrairement à un joueur de dé, comme le Chevalier de Méré), à la fin de mes soirées de joute, je verrais moyennement une fois pile à tous les 2 lancers.

Théoriquement tu peux être très mal chanceux et faire 100 jets "face" à la suite.

Ouais pour cette partie, je te suis très bien. J'ai 1/2^100 chances que ça arrive. Pour 2 lancers, j'ai donc 1/2^2 chances d'avoir 2 "piles" donc 25%. La probabilité d'avoir au moins un "face" dans les 2 lancers serait donc de 75%. Si mes calculs sont bons, j'ai encire là un bug mental avec l'interprétation de ce 75% et sa pertinence dans la situation du Chevalier de Méré. Le coeur de mon nœud est donc dans cet énoncé : Comment peut-on avoir 75% de chances de tirer au moins 1 "face" dans 2 lancers alors que statistiquement, il y aura 1 "face" (et non .75 faces) de tirée par 2 lancers?. Je comprend que ce 75% n'a pas l'interprétation que je lui donne instinctivement (.75 faces pour 2 lancers) mais je n'arrive pas à mettre le doigt précisément sur le "pourquoi".

La réflexion du Chevalier de Méré est la suivante :

Si je lance un dé, j'ai, on l'a vu, une chance sur six de sortir un six, une chance sur six de sortir un cinq, une chance sur six de sortir un quatre et ainsi de suite. Supposons que ce soit le six qui m'intéresse et supposons aussi que je lance mon dé quatre fois de suite. Eh bien en ce cas, pense Méré, j'ai quatre fois une chance sur six de tirer un six. Ce que cela représente est facile à calculer, même pour un Chevalier avec un coup de vin dans le nez. Cela donne:
4 X 1/6 = 2/3

J'ai donc, conclut Méré, deux chances sur trois de tirer un six en lançant quatre fois de suite un dé.

La conclusion soulignée est de moi. Plutôt que de passer à un autre calcul comme le fait Blaise Pascal dans l'histoire, quelle est l'erreur de ce raisonnement, ou les raisons de son inadmissibilité?

C'est ce que tu sembles m'expliquer ci-bas :

En fait tu biaises en te disant que la proba d'obtenir un 6 est 1/6 pour un lancer, donc de (1/6)*4 pour 4 lancers. Il faudrait que tu te dises que c'est la proba de faire un 6 plus la proba de faire deux 6, plus la proba de faire trois 6 etc ... il y a la notion de "au moins" qui est importante.

Là où je ne te suis pas, c'est que le problème est justement de calculer la probabilité d'obtenir au moins un 6 (si le Chevalier de Méré sors plus d'un 6, il gagne tout de même, ou p-e même arrête de jouer après avoir sorti le premier 6). À l'inverse, si le Chevalier de Méré ne gagnait seulement que lorsqu'il n'avait qu'un seul 6, j'aurais compris qu'il aurait fallu soustraire à ce ~67% la probabilité d'obtenir deux 6, plus celle d'en obtenir 3, etc. Je ne comprend donc pas en quoi ton dernier raisonnement invalide la conclusion du Chevalier de Méré.

Amicalement,
Phil

[Jean-Francois]

Hello Philippe,

Très schématiquement, le truc est que si tu veux faire des calculs de probabilités il te faut envisager toutes les possibilités que te donne un lancer de 4 dés et non les possibilités que te donne 4 fois le lancer de un dé:
1-1-1-1 (pas de six)
1-1-1-2 (pas de six)
1-1-1-3 (pas de six)
1-1-1-4 (pas de six)
1-1-1-5 (pas de six)
1-1-1-6 (un six)
2-1-1-1 (pas de six)
etc.

Cette liste se simplifie évidemment mais elle n'est pas équivalente à: 1 chance sur 6 multiplié par quatre essais.

C'est plus évident pour pile ou face avec deux pièces:
P-P (pas de face)
P-F (un face)
F-P (un face)
F-F ((au moins) un face)

Tu as au moins un face dans trois cas sur quatre donc 75%.

Pour pile ou face avec trois pièces:
P-P-P
P-P-F
P-F-P
P-F-F
F-P-P
F-P-F
F-F-P
F-F-F

Les chances sont excellentes: 7 chances sur 8 d'avoir au moins un face mais c'est moins bon que si tu avais: 3 x 1 / 2 ce qui donne 1 et 1/2, ou 150% qui seraient supérieur à 100% (ou 1). En suivant le raisonnement de Méré, on devrait toujours gagner en pariant sur la sortie d'au moins un face sur trois lancers de pièces. Mais, ce n'est pas le cas.

Ca devrait être clair parce que très naïvement énoncé.... mais je peau-de-bananise peut-être quelque part.

Jean-François

[Denis]

Salut Phil,

Content que tu réapparaisses sur le forum. Je craignais que tu sois mort.

Tu dis :

Le coeur de mon nœud est donc dans cet énoncé : Comment peut-on avoir 75% de chances de tirer au moins 1 "face" dans 2 lancers alors que statistiquement, il y aura 1 "face" (et non .75 faces) de tirée par 2 lancers?. Je comprend que ce 75% n'a pas l'interprétation que je lui donne instinctivement (.75 faces pour 2 lancers) mais je n'arrive pas à mettre le doigt précisément sur le "pourquoi".

Tu confonds deux notions :

1) Le nombre moyen de faces qu'on obtient en deux lancers. C'est ton 1.

2) La probabilité d'avoir au moins une face en deux lancers. C'est ton 75%.

C'est plus évident pour pile ou face avec deux pièces:
P-P (pas de face)
P-F (un face)
F-P (un face)
F-F ((au moins) un face)

Notons X le nombre de faces obtenues en deux lancers. X peut prendre 3 valeurs différentes : 0, 1 ou 2. Les probabilités de ces 3 valeurs sont p(0) = ¼, p(1) = ½ et p(2) = ¼.

Cette distribution est illustrée par le "diagramme à bâtons" suivant :



En raisonnant directement sur le diagramme, on voit aisément que

P(au moins 1 face) = p(1) + p(2) = ¾ .

Ton 1, le nombre moyen (théorique) de faces, c'est la moyenne pondérée des valeurs possibles, chacune de ces valeurs étant comptée proportionnellement à sa probabilité. Techniquement, on l'appelle l'espérance mathématique de X et on la note E(X).

On trouve : E(X) = 0*p(0) + 1*p(1) + 2*p(2) = 1. C'est le centre de gravité du diagramme à bâtons, là où il faudrait mettre un pivot pourqu'il reste en équilibre.

Avec l'autre exemple où on lance un dé 4 fois et qu'on pose X = "nombre de 6", X peut prendre 5 valeurs possibles : 0, 1, 2, 3, et 4. Un petit calcul (voir la loi binomiale avec n = 4 et p = 1/6) donne :

p(0) = 625/1296
p(1) = 500/1296
p(2) = 150/1296
p(3) = 20/1296
p(4) = 1/1296



En raisonnant comme pour la cas d'avant, on trouve que :

P(au moins un 6) = p(1) + p(2) + p(3) + p(4) = 1 - p(0) = 671/1296 ≈ 51.775%

et

Nombre moyen de 6 = E(X) = somme des valeurs possibles multipliées par leur probabilité
= 0*625/1296 + 1*500/1296 + 2*150/1296 + 3*20/1296 + 4*1/1296
= 864/1296
= 2/3.

C'est le centre de gravité du diagramme à bâtons, là où il faudrait placer un pivot pour qu'il tienne en équilibre.

J'ai peut-être compliqué inutilement mes explications, mais mon idée principale c'est que, comme j'ai dit au début, tu as confondu la probabilité d'avoir au moins un "succès" et le nombre moyen (théorique) de succès.

Ah! Tu m'as rappelé le bon vieux temps. Merci.

Denis

[PhilippeL]

Salut à J-F et Denis,

Grâce à vous, je peux à nouveau jouir de la vie!

Tout est crystal clear maintenant! Le chevalier de méré gagne ~52% du temps et comme ses gains seront toujours constants plutôt que pondérés au nombre de 6 tirés (puisque la définition d'obtenir un succès dans ce cas est seulement de tirer au moins un 6), l'espérance de gain de ~.67 ne change absolument rien.

Si je meurs ce soir d'un infarctus pendant que je déblais ma voiture, et bien je mourrai moins tordu que si la même situation était arrivée hier.

Merci

Amicalement,
Phil

[Denis]

Salut Phil,

Tu dis :

Grâce à vous, je peux à nouveau jouir de la vie!

(...)

Si je meurs ce soir d'un infarctus pendant que je déblais ma voiture, et bien je mourrai moins tordu que si la même situation était arrivée hier.

Merci

Je comprends ton enthousiasme, mais n'en fais pas un infarctus.

Moi aussi je trouve que quand on comprend mieux quelque chose qu'on comprenait moins bien, ça procure une sensation plaisante. Moralement.

J'ai bien du mal à comprendre ceux qui n'aiment pas cette sensation. Je parle des gens qui n'aiment pas le Redico.

Parlant de Redico, notre partie record de tous les temps, (629 propositions) est en danger de perdre sa place. Celle que je tiens présentement avec Feel (surtout sur le végétarisme) vient de coiffer la seconde plus longue (522), où tu étais aussi.

Le record sera-t-il battu ? Les paris sont ouverts.

J'ai une gomme à reprendre.

Denis