Statisticien demandé

[Kraepelin]

Mes statistiques sont loin. Je me demande dans quelle mesure les données significatives de cette épreuve sont significatives. J'aimerais me faire une échelle de grandeur facile à comprendre. Par exemple, cette corrélation est-elle aussi grande que la corrélation entre la taille et le poids d'une personne?

Risk of Postpartum Depressive Symptoms With Elevated Corticotropin-Releasing Hormone in Human Pregnancy
Ilona S. Yim, PhD; Laura M. Glynn, PhD; Christine Dunkel Schetter, PhD; Calvin J. Hobel, MD; Aleksandra Chicz-DeMet, PhD; Curt A. Sandman, PhD


Arch Gen Psychiatry. 2009;66(2):162-169.

Context Postpartum depression (PPD) is common and has serious implications for the mother and her newborn infant. A possible link between placental corticotropin-releasing hormone (pCRH) and PPD incidence has been hypothesized, but empirical evidence is lacking.

Objective To determine whether accelerated increases in pCRH throughout pregnancy are associated with PPD symptoms.

Design Pregnant women were recruited into this longitudinal cohort study. Blood samples were obtained at 15, 19, 25, 31, and 37 weeks' gestational age (GA) for assessment of pCRH, cortisol, and adrenocorticotropic hormone (ACTH). Depressive symptoms were assessed with a standardized questionnaire at the last 4 pregnancy visits and post partum.

Setting Subjects were recruited from 2 southern California medical centers, and visits were conducted in research laboratories.

Participants One hundred adult women with a singleton pregnancy.

Main Outcome Measure Symptoms of PPD were assessed at a mean (SD) of 8.7 (2.94) weeks after delivery with the Edinburgh Postnatal Depression Scale.

Results Sixteen women developed PPD symptoms. At 25 weeks' GA, pCRH was a strong predictor of PPD symptoms (R2 = 0.21; β = 0.46 [P < .001]), an effect that remained significant after controlling for prenatal depressive symptoms. No significant associations were found for cortisol and ACTH. Receiver operating characteristic curve analyses revealed that pCRH at 25 weeks' GA is a possible diagnostic tool (area under the curve, 0.78 [P = .001]). Sensitivity (0.75) and specificity (0.74) at the ideal cutoff point (pCRH, 56.86 pg/mL) were moderate. Growth curve analyses indicated that the trajectories of pCRH in women with PPD symptoms are significantly accelerated from 23 to 26 weeks' GA.

Conclusions At a critical period in midpregnancy, pCRH is a sensitive and specific early diagnostic test for PPD symptoms. If replicated, these results have implications for the identification and treatment of pregnant women at risk for PPD.

[Denis]

Salut Kraepelin,

À tort ou à raison, je me suis senti interpellé par ton titre.

Faute d'en savoir plus, j'ai un peu cherché sur le Web et le mieux que j'ai trouvé, c'est ça, qui est peut-être la source de ton copié-collé.

Je ne commenterai qu'un bout :

At 25 weeks' GA, pCRH was a strong predictor of PPD symptoms (R2 = 0.21; β = 0.46 [P < .001])

Je suppose qu'on a fait une régression linéaire simple et que ce qui est noté R2 est le coefficient de détermination, noté ici r2. Je suppose aussi que ce qui est noté β est le coefficient de corrélation lui-même (noté r ici). C'est d'ailleurs numériquement cohérent avec 0.21 = 0.462.

Si j'ai bien interprété le R2 et le β, le P < .001 est correct, compte tenu de la taille échantillonnale n = 100. En effet, ça mène à un T de 5.1 via



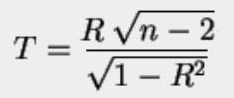
5.1, c'est très significatif pour une variable de Student à 98 degrés de liberté (très semblable à une N(0,1)).

Bien sûr, on dit : « If replicated, these results have implications for... ». Étant donné que l'hypothèse a été testée avec les données qui ont permis de la formuler (et que des zillions d'hypothèses auraient été formulables), faut se méfier et attendre une confirmation indépendante.

Mais je pense que ta question principale, c'est :

J'aimerais me faire une échelle de grandeur facile à comprendre. Par exemple, cette corrélation est-elle aussi grande que la corrélation entre la taille et le poids d'une personne?

Si tu veux te représenter à quel point une corrélation de 0.46 (i.e. R2 = 0.21), c'est "fort", imagine que tu lances 100 pièces de monnaie et que tu poses :

X = nombre de faces obtenues dans les 21 premiers lancers,
Y = nombre total de faces obtenues dans les 100 lancers.

Entre ces X et Y, le coefficient de détermination est de 21% (i.e. 21% de la variance de Y est attribuable à X) et le coefficient de corrélation est de 0.46.

Il s'agit d'une corrélation assez forte, mais pas décisive. Même si on connaît le nombre de faces obtenues dans les 21 premiers lancers, les 79 autres lancers peuvent sérieusement bousiller notre prédiction naturelle (X + 79/2) pour le nombre total de faces qu'on obtiendra pour les 100 lancers réunis.

Je ne sais pas ce que vaut le coefficient de corrélation entre la taille et le poids des personnes. Je suppose qu'il faudrait encadrer notre population, par exemple, ne considérer que des adultes de même sexe (et de même nation). Je ne sais pas s'il est plus grand que 0.46. J'ai l'impression que OUI mais, faute de données, ce n'est qu'un feeling.

Je ne sais pas non plus à quel point ma réponse te sera utile.

Je suppose "un tipeu".

Denis

[Kraepelin]

Si j'ai bien interprété le R2 et le β, le P < .001 est correct, compte tenu de la taille échantillonnale n = 100. En effet, ça mène à un T de 5.1 via



5.1, c'est très significatif pour une variable de Student à 98 degrés de liberté (très semblable à une N(0,1)).

Si tu veux te représenter à quel point une corrélation de 0.46 (i.e. R2 = 0.21), c'est "fort", imagine que tu lances 100 pièces de monnaie et que tu poses :

X = nombre de faces obtenues dans les 21 premiers lancers,
Y = nombre total de faces obtenues dans les 100 lancers.

Entre ces X et Y, le coefficient de détermination est de 21% (i.e. 21% de la variance de Y est attribuable à X) et le coefficient de corrélation est de 0.46.

Il s'agit d'une corrélation assez forte, mais pas décisive. Même si on connaît le nombre de faces obtenues dans les 21 premiers lancers, les 79 autres lancers peuvent sérieusement bousiller notre prédiction naturelle (X + 79/2) pour le nombre total de faces qu'on obtiendra pour les 100 lancers réunis.

Je ne sais pas non plus à quel point ma réponse te sera utile.

Je suppose "un tipeu".

Denis

Salut Denis

Très utile ta réponse. Ça m'évite de remmetre le nez dans mes vieux livres.

Merci!