La terre creuse

[mf9000]

Très intéressant...

Il manque cependant un élément pour compléter le modèle : la rotation de la Terre crée une force centrifuge... Comment interagit-elle avec la force d'attraction à l'intérieur de la sphère ?

Il est bien certain que cette force, nous la subissons aussi (nous pauvres humains de l'extérieur de la Terre) et qu'elle n'est pas suffisante pour nous faire décoller, par conséquent elle n'est sans doute pas non plus assez forte pour coller les zitis de l'intérieur de la Terre contre les hypothétiques parois internes...

Cela rejoint un autre problème de physique qui m'intrigue en SF : est-il réellement envisageable de recréer une pseudo-gravité en faisant tourner un vaisseau spatial sur lui-même, comme dans Rama ou 2001 ? À quelle vitesse doit tourner un tel vaisseau, pour quel diamètre, pour que se crée une gravité supportable par vous et moi ?

[richard]

À quelle vitesse doit tourner un tel vaisseau, pour quel diamètre, pour que se crée une gravité supportable par vous et moi ?

Pour un diamètre de 110m je trouve qu'il doit tourner à 4 tour/mn pour avoir l'équivalent de la gravité terrestre.
"Idéalement, le taux de rotation doit être inférieur à 2 tr/min pour réduire les effets des forces de Coriolis. Pour simuler une gravité similaire à la gravité terrestre (1 g), le rayon doit être d'au moins 224 m, ce qui représente un gros vaisseau spatial. Pour réduire sa masse, il pourrait être constitué de deux éléments reliés par un câble (par exemple, une partie pour l'habitation, et une autre pour le reste)." http://fr.wikipedia.org/wiki/Gravit%C3%A9_artificielle

[curieux]

Salut mf900 et les autres aussi oeuf corse...

ça aussi c'est un problème interressant mais il ne faut pas perdre de vue que pour ressentir une force qui ressemble à la gravitation, il faut que les objets soit d'abord scotchés à la paroi qui va entrer en rotation. Sinon la sphère tournera et ils resteront en apesanteur dans l'espace intérieur.

En parlant d'apesanteur, merci en passant à Denis pour sa démo, dans le cas d'une Terre en forme de coquille d'oeuf creuse, ce serait l'apesanteur pour tous les objets dès qu'ils seraient dans le volume creux, c'est à dire dès qu'ils quitteraient la face interne de la coquille. S'ils n'étaient pas attachés à la surface, un bon coup de talon et ils se rendraient sans peine à l'opposé. La seule force d'attraction étant celle de la masse d'air occupant l'espace creux.
Exception faite des forces provoquées par les astres, Soleil et lune ainsi que les variations de masses aléatoires dûes aux marées.
Cela change un peu de la force décroissante à laquelle serait soumise un objet qui se dirigerait à l'intérieur d'un tunnel hypothètique passant par le centre de la Terre.

[embtw]

Salut mf900 et les autres aussi oeuf corse...

ça aussi c'est un problème interressant mais il ne faut pas perdre de vue que pour ressentir une force qui ressemble à la gravitation, il faut que les objets soit d'abord scotchés à la paroi qui va entrer en rotation. Sinon la sphère tournera et ils resteront en apesanteur dans l'espace intérieur.

Salut Curieux,

Donc, si je suis ton raisonnement et suppose qu'un vaisseau spatial a les dimensions et la technologie requises pour simuler la gravitation, les gens dedans sont sur la paroi et le bazar commence à tourner et simule la gravité.

Si à ce moment précis, les gens sautent en l'air, alors ils se retrouvent hors gravitation en apesanteur et s'ils sautent suffisamment fort, ils vont aller en direction de ce qui est leur plafond, qu'ils font finir par toucher et ils vont donc s'écraser comme une grosse m**** , non, puisqu'à ce moment précis, ils seront de nouveau solidaires à la paroi ?

[curieux]

c'est compliqué à deviner ce qui se passerait, si le gars est en rotation, il a une vitesse, en sautant sa vitesse par rapport à la coque ne change pas, il 'retombe' donc sur la coque. C'est la cas du manège qu'on trouvait dans le temps sur les foires.
Pour que ça reste vrai, il faut que le diamètre de la coque soit assez grand par rapport à la hauteur du gars.
Si le diamètre est faible, ça se gâte, la force ressentie par la tête est plus petite que celle ressentie par les pieds du bonhomme.

[Denis]

Salut embtw,

À propos de "ma" démonstration, tu dis :

J'ai du apprendre cela, il y a longtemps, mais je ne m'en souviens pas et je n'ai plus mes livres de maths du lycée. Du coup, si cela n'est pas trop contraignant pour toi en terme de temps, pour ma culture, je suis intéressé par les raisonnements.

Tu me dis que, dans ma démonstration, un bout où tu ne vois pas net, c'est ça :

Via quelques petits raisonnements de géométrie élémentaire, on peut montrer (au besoin, j'essayerai de mieux le justifier) que les aires S1 et S2 sont proportionnelles aux carrés des distances D1 et D2.

OK. Je vais essayer d'être plus clair, afin d'éviter cette situation-là.

Je rappelle le diagramme de base :



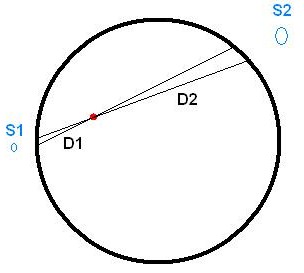
et je rappelle que le double-cône originaire du point rouge est très très fin. Infinitésimalement fin.

On veut montrer que les aires S1 et S2 des deux ellipses tracées par les cônes sur la surface de la sphère sont proportionnelles aux carrés de leurs distances (D1 et D2) au point rouge.

Pour ça, on aura besoin de quelques petits résultats préliminaires :

1) Quand un cylindre rencontre un plan, ça trace une ellipse dont la forme (son excentricité ou, si tu préfères, le rapport entre le grand et le petit diamètre de l'ellipse) ne dépend que de l'angle entre le cylindre et le plan.

Si le cylindre frappe à 90°, ça va faire un cercle. S'il arrive très rasant, ça va faire une ellipse très allongée. S'il arrive à 30°, l'ellipse sera 2 fois plus longue que large. C'est une affaire de sinus.

2) Quand on a toute une famille de formes semblables, leurs aires sont proportionnelles aux carrés de leurs "diamètres".



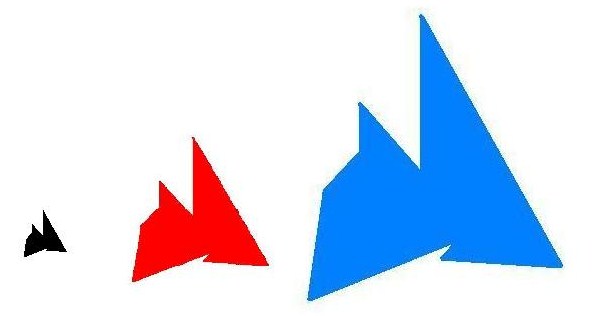
3) Quand on trace une corde dans un cercle, elle rencontre la circonférence du cercle avec des angles égaux (en vert).



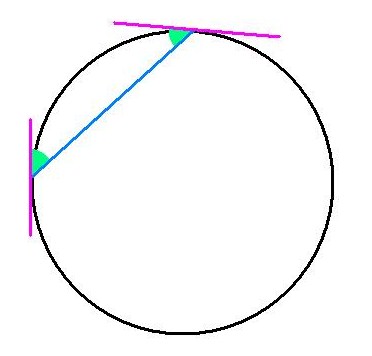
4) Localement, un cône ultra-fin se comporte comme un cylindre dont le diamètre est proportionnel à la distance à la pointe du cône (le point rouge).

5) Localement, la surface d'une sphère se comporte comme un plan.

Bon. On a tous les ingrédients pour achever notre gâteau : voir que les aires S1 et S2 sont proportionnelles aux carrés des distances (D1² et D2²).

La clé est peut-être de remarquer que le petit diamètre des ellipse est simplement la largeur du cône à la distance D du point rouge.

Si c'est toujours pas clair, je peux essayer de faire mieux.

Denis

P.S. Ces résultats-là sont loin d'être nouveaux. Ça remonte à quelques années après Newton. Sinon à Newton lui-même.

[embtw]

Salut embtw,

À propos de "ma" démonstration, tu dis :

Démontration

Salut Denis,

Merci pour ces explications, je vais me les approprier dans un moment de calme.

Pourrais-tu en sus, me conseiller, sur un livre ( ou plusieurs ) de préférence en français ( je parle et lis bien l'anglais mais je préfère le français quand je ne maitrise pas le contenu ) me permettant de renouer avec les concepts mathématiques en trigonométrie et en probabilité.

Note : Pour moi, comparativement, Newton est aussi loin que mes 16/17 ans où j'ai appris ces choses-là ( Pas exactement aussi loin, mais presque )

[Denis]

Salut embtw,

Je n'ai pas vraiment de livres à te conseiller. Tes deux thèmes (trigonométrie et probabilités) sont pas mal vastes et je suppose qu'il faut partir au début.

Je pense que le mieux, c'est que tu trouves ça sur le net. Par exemple, sur Wikipedia.

http://fr.wikipedia.org/wiki/Trigonom%C3%A9trie

http://fr.wikipedia.org/wiki/Th%C3%A9or ... lit%C3%A9s

Il y a probablement mieux que Wikipedia. Faudrait chercher.

Si ce qui t'intéresse, c'est surtout les applications des maths en physique newtonienne, il y aurait ça :

http://fr.wikipedia.org/wiki/Physique_newtonienne

Il y a aussi les lois de Kepler qui méritent d'être connues.

http://fr.wikipedia.org/wiki/Lois_de_Kepler

Pas d'autres idées pour le moment.

Denis

[mf9000]

Merci pour vos réponses... J'avoue qu'en physique j'ai toujours eu un problème avec les forces dites "fictives", de type justement, centrifuge ou Coriolis. Mais je me soigne