Causalité

[Jean-Francois]

Question du sondage:

Des chercheurs étudient l’effet d’un médicament (M) sur un symptôme (S). Pour ce faire, ils partagent leurs sujets d’étude en deux groupes, l’un auquel ils donnent M et l’autre auquel ils donnent un placebo (P). Ils observent que :
- dans le premier groupe (avec M), 68 sujets ne montrent pas le symptôme S et 17 sujets montrent S;
- dans le second groupe (avec P, sans M), 16 sujets ne montrent pas S et 4 montrent S.
Selon vous, ces résultats indiquent que :
1. M atténue S
2. M aggrave S
3. M n’a pas d’effet notable sur S
4. Il faudrait avoir plus de sujets pour se faire une idée de l’effet de M sur S
5. Les expériences sur les médicaments sont toutes truquées

Justifiez pourquoi vous avez raison si vous le voulez

[Dash]

1- les 2 groupes ne sont pas égaux,
2- mais en %, il y a 20% dans tous les cas qui ont des symptômes.

A priori (pas bcp de temps, je dois quitter), je dirais qu'avec ou sans medoc, puisque le même pourcentage de sujet a des symptômes dans les 2 groupes, que M n’a pas d’effet notable sur S.

Mais bon, je ne sais pas s'il nécessite un nombre minimum de sujets, pour ce type d'étude, afin que ce soit significatif (échantillons représentatifs de la population, etc.).

[Kraepelin]

Salut

Pour répondre, il faut présumer que le reste de la méthodologie (que tu ne décris pas) est bonne.

Si on pose S/non S, dans les deux groupes ont obtient 0,25. La bonne réponse semble, "pas d'effet de M".

C'est trop facile, alors je me méfis (je suis conpirationniste après tout).

L'échantillon est petit (et les groupes inégaux) mais probablement suffisant pour une comparaison de mesures OUI/NON

C'est un piège pour ceux qui ont oublié leurs cours de statistiques? Où est l'os?

[Nicolas78]

Il faudrait connaitre le nombres de personnes dans chaque groupes pour donner un avis, dans le sens ou ils sont différents, il faudrait faire plus de groupes et plus de test. Avec des groupes, si possibles, asses équivalents.
De plus, dans le groupe M, 17 sujets montrent des symptômes, alors que dans le groupe P, 4 "seulement". Sans proportionnelle.
Pour savoir quel est l'effet placebo dans chaque groupe (car un médicament actif a aussi un effet placebo), il faudrait répéter plusieurs fois l'expérience avec des groupes de tailles plus uniformes. Il faut aussi prendre en compte de quelle maladie on parle, et si les groupes sont testés au même stade de la maladie, car les guérisons "naturelles" peuvent faire croire qu'il existe un effet placebo et même un effet médicamenteux alors que ce n'est pas forcement le cas.
Ca me parait pas possible de voter en l'état de l'énoncé, sauf a résumer le soucis a "Il faudrait avoir plus de sujets pour se faire une idée de l’effet de M sur S". Même si en fait il faudrait plus d'infos sur la situation.
Au niveau proportionnel, cependant, M ne semble pas se sentir mieux que P...

[LoutredeMer]

Je n'ai pas lu les réponses des autres intervenants pour ne pas être influencée.

Ma réponse est :

Spoiler

Afficher

4. Il faudrait avoir plus de sujets pour se faire une idée de l’effet de M sur S
parce que :

- D'abord, je ne comprends pas pourquoi il a plus de sujets dans le groupe expérimental que dans le groupe témoin (85 contre 20).

- Ensuite, je pense qu'il devrait y avoir un 3ème groupe qui ne prend rien, ni M ni P (je crois qui'l porte un nom mais je ne sais plus lequel). Puisqu'il peut y avoir des sympômes (et des maladies) qui disparaissent d'eux-memes au bout de quelques jours.

[spin-up]

Selon vous, ces résultats indiquent que :
1. M atténue S
2. M aggrave S
3. M n’a pas d’effet notable sur S
4. Il faudrait avoir plus de sujets pour se faire une idée de l’effet de M sur S
5. Les expériences sur les médicaments sont toutes truquées

Justifiez pourquoi vous avez raison si vous le voulez

Spoiler

Afficher

Tout ce qu'on peut dire avec certitude c'est que ces résultat ne montrent pas d'effet de M sur S (ce qui n'est pas equivalent a 3.). Et que celui qui a conçu l'étude devrait changer de carrière.

Je suis nul en stats mais on peut montrer de façon assez simple que l’échantillon est trop faible pour mettre en evidence un éventuel effet. Le problème le plus évident est la taille du groupe contrôle (16)et le nombre de cas avec S dans ce groupe (4, soit 20%).

2 exemples simples:

Cas 1) Admettons que l'incidence réelle de S soit de 40%. Il n'est pas rare d'obtenir un groupe contrôle avec 4 sujets sur 20 présentant S.
Auquel cas, le groupe traité devrait avoir en moyenne 34 sujets avec S en absence d'effet. Mais il en a seulement 17, donc, potentiellement, M réduit l'incidence de S d'un facteur 2 (ce qui est un effet honorable).

Cas 2) Admettons cette fois que l'incidence réelle de S soit de 10%. La non plus, il n'est pas rare d'obtenir un groupe contrôle avec 4 sujets sur 20 présentant S.
Auquel cas, le groupe traité devrait avoir en moyenne 8.5 sujets avec S en absence d'effet. Mais il en a 17, donc potentiellement, M augmente l'incidence de S d'un facteur 2 (ce qui est inquiétant).

Conclusion: Ces résultats ne permettent pas de montrer un effet de M , mais ne montrent pas non plus l'absence d'un effet positif ou négatif.

[Jean-Francois]

Tout ce qu'on peut dire avec certitude c'est que ces résultat ne montrent pas d'effet de M sur S (ce qui n'est pas equivalent a 3.). Et que celui qui a conçu l'étude devrait changer de carrière

Si les résultats étaient:
- Avec M, 80 ne montrent pas S et 5 montrent S;
- Sans M, 5 ne montrent pas S et 15 montrent S.
Tu n'y verrais pas d'indication d'un effet causal de M sur S?

on peut dire avec certitude c'est que ces résultat ne montrent pas d'effet de M sur S (ce qui n'est pas equivalent a ["les résultats indiquent que M n’a pas d’effet notable sur S"])

J'ai remplacé "3)" dans ta phrase par la proposition 3. S'il y a une différence entre ta formulation et la mienne, elle me parait franchement subtile, limite tétracapillotomiesque.

Jean-François

[spin-up]

Tout ce qu'on peut dire avec certitude c'est que ces résultat ne montrent pas d'effet de M sur S (ce qui n'est pas equivalent a 3.). Et que celui qui a conçu l'étude devrait changer de carrière

Si les résultats étaient:
- Avec M, 80 ne montrent pas S et 5 montrent S;
- Sans M, 5 ne montrent pas S et 15 montrent S.
Tu n'y verrais pas d'indication d'un effet causal de M sur S?

Dans ce cas, si, ca semble indiquer qu'il existe un effet causal.

on peut dire avec certitude c'est que ces résultat ne montrent pas d'effet de M sur S (ce qui n'est pas equivalent a ["les résultats indiquent que M n’a pas d’effet notable sur S"])

J'ai remplacé "3)" dans ta phrase par la proposition 3. S'il y a une différence entre ta formulation et la mienne, elle me parait franchement subtile, limite tétracapillotomiesque.

Jean-François

Je ne suis pas d'accord, la difference est importante. Mes 2 exemples montrent justement qu'il est plausible qu'un effet notable existe avec ces résultats.
Si tu multiplies tous les nombres de ton exemple par 100 ou meme par 10, la on est d'accord: l'experience indique une absence d'effet notable.

[Jean-Francois]

Dans ce cas, si, ca semble indiquer qu'il existe un effet causal.
[...]
Si tu multiplies tous les nombres de ton exemple par 100 ou meme par 10, la on est d'accord: l'experience indique une absence d'effet notable.

Àma, soit tu acceptes que l'expérience telle qu'elle est décrite (i.e., sans détails) donne des résultats interprétables (ligne du haut), soit tu défends qu'on ne peut pas en tirer la moindre interprétation (ligne du bas). Mais critiquer la valeur intrinsèque de l'expérience en fonction des résultats (ici, en référant au nombre de sujets qui serait suffisant ou insuffisant selon l'interprétation), c'est changer de place les poteaux des buts. En d'autres termes, si l'expérience peut indiquer un effet causal, elle peut aussi indiquer une absence d'effet. (Absence d'effet qui n'est pas absolue: c'est juste ce que ces résultats indiquent/suggèrent/pointent vers elle.)

J'ai lu tes exemples mais, outre que tu sors du cadre de l'énoncé, ce que tu me sembles défendre c'est "M n'a [absolument aucun] effet sur S". Sauf que la proposition 3 n'est pas affirmative sur ce point: elle dit juste que "ces résultats indiquent que M n'a pas d'effet sur S". Elle n'empêche pas que d'autres résultats puissent montrer que "M n'a [absolument aucun] effet sur S".

Tu peux voir ça comme:
H0: M n'a pas d'effet sur S.
H1: M a un effet [atténuant/aggravant] sur S.
Si p est > 0,3*, on garde H0.

Jean-François

* Par exemple.

[curieux]

Salut à tous

En l'état du test, le médicament est équivalent au placébo (*), donc je réponds (3) : aucun effet.
On n'a droit qu'à une réponse, on ne peut donc pas répondre (4) sans avoir d'abord répondu (3) puisque c'est une déduction issue du constat de l'équivalence médicament=placébo.
Si j'avais droit à 2 réponses alors je dirais, dans l'ordre : (3) et (4)

(*) 16/4 = 68/17 = 4/1

[Etienne Beauman]

Salut à tous

En l'état du test, le médicament est équivalent au placébo (*), donc je réponds (3) : aucun effet.
On n'a droit qu'à une réponse, on ne peut donc pas répondre (4) sans avoir d'abord répondu (3) puisque c'est une déduction issue du constat de l'équivalence médicament=placébo.
Si j'avais droit à 2 réponses alors je dirais, dans l'ordre : (3) et (4)

(*) 16/4 = 68/17 = 4/1

J'aurai pas mieux dit ce que j'en penses !

[Jean-Francois]

Si j'avais droit à 2 réponses alors je dirais, dans l'ordre : (3) et (4)

À mon avis, si on était sur un forum plus représentatif de la population en général (et qu'on ne laissait pas accès aux réponses pour pas influencer ceux qui n'ont pas encore voté), l'ordre des réponses au sondage serait 1 > 3 > 4 > 5 > 6 J'expliquerai le but de celui-ci plus tard (ça a un rapport avec la causalité*).

Sinon, j'ai testé statistiquement les deux groupes (85 avec M c. 20 sans M) en mettant 0 pour "sans S" et 1 pour "avec S" en utilisant deux tests de t (non paramétriques). La disparité entre les groupes n'empêche pas de calculer que "68/17" et "16/4" donne un p > 0,95. Pour les proportions "80/5" et "5/15", c'est p < 0,0001. Y'a pas photo.

Jean-François

* Je vous assure, bande de sceptiques.

[Dash]

Salut à tous

En l'état du test, le médicament est équivalent au placébo (*), donc je réponds (3) : aucun effet.
On n'a droit qu'à une réponse, on ne peut donc pas répondre (4) sans avoir d'abord répondu (3) puisque c'est une déduction issue du constat de l'équivalence médicament=placébo.
Si j'avais droit à 2 réponses alors je dirais, dans l'ordre : (3) et (4)

(*) 16/4 = 68/17 = 4/1

J'aurai pas mieux dit ce que j'en penses !

Oui, dans les 2 cas (groupes) en calculant de cette façon, ça fait du 4 pour 1 (ou 1 pour 4 dépendamment si l'on considère les symptomatiques ou les autres), mais moi j'ai préféré divisé par le total des sujets (de chacun des groupes) pour ensuite multiplier par 100 afin de me représenter en pourcentage, ce qui donne 20%, donc du 1 pour 5 (ou 5 pour 1 dépendamment si l'on considère les symptomatiques ou les autres).

Question (suis pas très calé en math/stats) : même si les deux façons de calculer permettent d'obtenir une égalité entre les deux groupes pour conclure qu'il n'y a pas de différence, n'est-il pas mieux de se représenter le ratio sur le nombre total de sujets pour chaque groupe? Parce que 20% (ou 80%), ça ne représente pas 25% (ou 75%).

À mon sens, c'est bien 20 % des sujets des deux groupes qui ont des symptômes (ou 80% qui n'en ont pas). Votre 25% (ou 75%) ne peut-il pas induire un biais de fausse représentativité~ratio même s’il permet, dans le cadre de cet exercice, d'aboutir à la même conclusion quant à la question posée?

[Dash]

Oubliez mon post précédant...

En réalité, un pour/contre quatre veut dire/implique un sur 5, etc.

Mon "un pour 5" était faux.

[jean7]

Ce n'est pas la peine de perdre du temps à continuer à étudier l'effet de M sur S.
Cet effet a eu l'occasion de s'exprimer.

Le résultat est suspect car on s'attendrait à un petit écart de résultat entre les deux groupes, mais bon, ça aussi ça peut arriver.

[Dash]

Pour ce faire, ils partagent leurs sujets d’étude en deux groupes...

Quel est l'intérêt de ne pas partager les groupes de façon égale?



Moins il y a de sujets, moins c'est représentatif, non ? Enfin, je sais que si les sujets d''un sondage sont bien réparties et choisi au hasard, c'est ok, mais pour un groupe d'uniquement 20 sujets, la marge d'erreur n'est-elle pas trop importante? Pour des études en double aveugle concernant des médocs?

Il y avait 105 sujets dispo au total, pourquoi ne pas avoir fait un groupe de 52 et un groupe de 53?

Nécéssairement moins il y a de sujets, moins le résultat sera précis, non?

Imaginons un groupe de 103 et un groupe de 2. Pour ce dernier, les seuls résulats possible seront 100%, 0% ou 50% des sujets sont bla-bla-bla.

[Dash]

Imaginons un groupe de 103 et un groupe de 2. Pour ce dernier, les seuls résulats possible seront 100%, 0% ou 50% des sujets sont bla-bla-bla.

La plus petite valeurs possible - sauf zéro - par nombre de sujets dans un groupe :

2 - 50%
3 - 33,3%
4 - 25%
5 - 20%
6 - 16.6%
etc, etc..
20 - 5%
etc, etc..
53 - 1,88%
etc, etc..
85 - 1,17%

Donc j'imagine que la marge d'erreur est acceptable à cette "précision"?

Mais dans le groupe de 85 sujets, la plus petite valeur possible est de 1,17% Donc les chercheurs considèrent que la différence entre 1~5% est négligeable?

J'arrives tjrs pas à piger pourquoi ne pas avoir fait un groupe de 52 et un groupe de 53, étant donné que la plus petite valeurs aurait été de 1,88%

....hâ, ok, parcequ,'on aurait pas pu savoir si elle atteignait moins de 1,9%, c'est ça? Faut donc un juste millieu entre grand/petit groupe, assez pour être précis, mais aussi pour aller jusqu'à une certaine très petite valeur, c'est pour ça? 1% est un seuil pour ce type d'étude j'imagine. Donc avec 105 sujets, quand on doit faire 2 groupes, on doit faire un groupe de 85 sujets afin d'observer le seuil de 1%, c'est ça?

[Etienne Beauman]

Quel est l'intérêt de ne pas partager les groupes de façon égale?

Si le traitement s'avère efficace c'est pas plus mal que le groupe qui le prends soit plus important que celui qui prends le placebo.

Après faut balancer avec les effets secondaires, mais si c'est une molécule déjà connue on connait normalement bien le sujet.

[Dash]

Si le traitement s'avère efficace c'est pas plus mal que le groupe qui le prends soit plus important que celui qui prends le placebo.

Ouais, ça fait sens.

[Jean-Francois]

Mon "un pour 5" était faux.

En fait, c'est légèrement plus juste que 1/4. En %, cela correspond à la probabilité qu'aucun effet ne soit observé* si M est présent (=17/(68+17)) ou si M est absent (=4/(16+4)). Ces probabilités sont de 20% que M soit présent ou non, donc elles s'annulent. On peut aussi utiliser les probabilités inverses (80%) qui correspondent à un effet de M ou de l'absence de M. En tant que méthode d'approximation, le ratio est une bonne approche: ce qui est important est de comparer l'ensemble des 2 groupes. Et c'est ce que de nombreuses personnes n'ont pas tendance à faire.

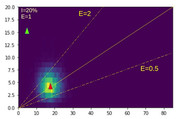
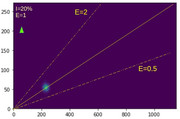
Sur le plan des probabilités, la matrice 68 / 17 / 16 /4 ne diffère pas vraiment de 1156 / 289 / 272 / 68 (j'ai multiplié par 17). Mais 1156 est largement supérieur à 68 ce qui donne l'impression que, dans le second cas, il y a un fort effet de M.

Le chiffre que les gens oublient souvent est le "4" (i.e., qui correspond à une absence d'effet quand M est absent) et tendent à faire des comparaisons intuitives (i.e., rapides) entre un effet de M (68) et soit l'absence d'effet (17), soit l'effet quand M est absent (16). Des études montrent que plus la différence est grande dans ces comparaisons (ex., 68-17 << 1156-289 ou 68-16 << 1156-272), plus les gens ont tendance à conclure à un lien causal. Mettre en évidence ce biais cognitif est l'intérêt de ne pas faire des groupes égaux (ce qui n'empêche pas que la répartition permet des inférences statistiques**).

Il y a autre chose à dire mais je n'ai pas le temps de le faire maintenant.

Jean-François

* Pour simplifier la description, je prends une absence de S comme un effet.
** Bien entendu, s'il fallait penser "irl", il faudrait que les groupes soient randomisés, équivalents en termes de sexe/âge/condition/etc., et on garde tous les sujets qui ont terminé l'étude. On n'est pas chez Rapult, on cherche pas à prétendre que M a un effet malgré que les résultats ne suivent pas

[spin-up]

Àma, soit tu acceptes que l'expérience telle qu'elle est décrite (i.e., sans détails) donne des résultats interprétables (ligne du haut), soit tu défends qu'on ne peut pas en tirer la moindre interprétation (ligne du bas). Mais critiquer la valeur intrinsèque de l'expérience en fonction des résultats (ici, en référant au nombre de sujets qui serait suffisant ou insuffisant selon l'interprétation), c'est changer de place les poteaux des buts. En d'autres termes, si l'expérience peut indiquer un effet causal, elle peut aussi indiquer une absence d'effet. (Absence d'effet qui n'est pas absolue: c'est juste ce que ces résultats indiquent/suggèrent/pointent vers elle.)

Non je ne déplace pas vraiment les poteaux.
Le protocole expérimental n'est pas égal vis a vis de toutes les situations.
Pour le cas 80/5 et 5/15, il quasi-impossible que ce soit du au hasard (càd d'obtenir ces résultats avec un medicament sans effet). L'echantillon est suffisant pour conclure a l'existence d'un effet.
Pour le cas, 68/17 et 16/4, il est tout a fait possible d'obtenir ces résultats avec un médicament qui a un effet.

J'ai fait des simulations Monte Carlo en utilisant un groupe controle de 20 et un groupe traité de 85, et en faisant 10000 experiences:
I: incidence du symptome S sans traitement
E: effet du medicament. Si E=2, le médicament divise l'incidence de S par 2. Si E=1/2 l'incidence de S est multipliée. E=1 est une absence d'effet.

Voila par exemple avec I=20% et E=1 (pas d'effet). La "tache" montre la distribution des resultats. Le triangle rouge montre le résultat "68/17 et 16/4" , le triangle vert montre le résultat "80/5 et 5/15". la ligne jaune est la ligne d'absence d'effet.

Sur le plan des probabilités, la matrice 68 / 17 / 16 /4 ne diffère pas vraiment de 1156 / 289 / 272 / 68 (j'ai multiplié par 17). Mais 1156 est largement supérieur à 68 ce qui donne l'impression que, dans le second cas, il y a un fort effet de M.

Pourtant statistiquement, le grand groupe exclut de facon beaucoup plus certaine l'existence d'un effet notable. Sur la simulation MC, la tache est beaucoup plus petite.

[Dash]

Sur le plan des probabilités, la matrice 68 / 17 / 16 /4 ne diffère pas vraiment de 1156 / 289 / 272 / 68 (j'ai multiplié par 17). Mais 1156 est largement supérieur à 68 ce qui donne l'impression que, dans le second cas, il y a un fort effet de M.

Pourtant statistiquement, le grand groupe exclut de facon beaucoup plus certaine l'existence d'un effet notable. Sur la simulation MC, la tache est beaucoup plus petite.

Ce qui revient à dire ce que je disais sur la « résolution » qu'implique le nombre de sujets, non? Sinon, c'est sur qu'en observant a posteriori des résultats au % identiques dans 2 groupes aux nombres de sujets différents, l'on pourra tjrs dire que la matrice et le rapport ne changent pas, mais le dire après coup pour des % identique, ça s'apparente au biais rétrospectif, non?

Faudrait refaire de multiples occurrences d'expériences avec différentes matrices pour s'assurer que le rapport est toujours sensiblement similaire, non?

[spin-up]

Le chiffre que les gens oublient souvent est le "4" (i.e., qui correspond à une absence d'effet quand M est absent) et tendent à faire des comparaisons intuitives (i.e., rapides) entre un effet de M (68) et soit l'absence d'effet (17), soit l'effet quand M est absent (16). Des études montrent que plus la différence est grande dans ces comparaisons (ex., 68-17 << 1156-289 ou 68-16 << 1156-272), plus les gens ont tendance à conclure à un lien causal. Mettre en évidence ce biais cognitif est l'intérêt de ne pas faire des groupes égaux (ce qui n'empêche pas que la répartition permet des inférences statistiques**).

Ok, je vois mieux ou tu veux en venir, tu ne veux pas parler de stats.
Dit autrement, pour n'importe quelle experience et quels que soient les résultats, il existe une facon de presenter les résultats pour faire croire ce qu'on veut a un grand nombre de gens.

[Jean-Francois]

Pour le cas, 68/17 et 16/4, il est tout a fait possible d'obtenir ces résultats avec un médicament qui a un effet.

Sauf que si on prend ces résultats sans chercher à les surinterpréter, on peut très bien dire que à leur vue le médicament n'a pas d'effet*. C'est même la chose la plus prudente à faire puisqu'on ne peut pas dire qu'il y a un effet. Et dire que l'expérience ne démontre pas d'effet n'est pas affirmer qu'il est impossible de démontrer un éventuel effet (les homéopathes sont très bons pour les conclusions sous forme de "il faut d'autres études" ).

Personne ne nie qu'il faudrait faire d'autres expériences/d'autre sujets pour déterminer avec plus de précision si M a ou pas un effet, mais insister là-dessus c'est changer les données de la question. (D'ailleurs, on peut aussi choisir l'option 4 (mais t'a(vai)s pas voté). Et, comme Curieux et Étienne, je pense que l'ordre devrait être 3 > 4.)

Pourtant statistiquement, le grand groupe exclut de facon beaucoup plus certaine l'existence d'un effet notable

C'est effectivement le cas dans certains exemples (et c'est pourquoi le raccourci heuristique des fractions n'est pas toujours juste). Maintenant, les résultats dont il est question dans le sondage sont ceux de la matrice précédente.

Note aussi que je doute que la plupart des gens ont les connaissances et moyens de faire des simulations Monte Carlo. Tout comme la plupart des gens n'ont pas ta compréhension "professionnelle" des liens causaux.

Jean-François

* Tu peux tourner les phrases comme tu le souhaites vu que ta critique est essentiellement sémantique.

[spin-up]

Sauf que si on prend ces résultats sans chercher à les surinterpréter, on peut très bien dire que à leur vue le médicament n'a pas d'effet*. C'est même la chose la plus prudente à faire puisqu'on ne peut pas dire qu'il y a un effet.

OK avec ca. C'est juste moi qui avait mal compris le but de l'exercice.