L'échelle temporelle logarithmique
Publié : 16 avr. 2010, 08:58
Salut S.C.
Merci pour ta réponse. Mieux vaut tard que jamais.
Tu dis :
Si on tient à donner un nom à ses unités, on n'a qu'à leur en donner un, comme on fait pour les décibels.
Pourquoi pas des "ères logarithmiques", ou des "années logarithmiques", dans le cas où on ajuste les paramètres de telle sorte que les deux échelles se confondent dans le voisinage de maintenant.
À propos de la fonction qui passe de l'échelle linéaire à l'autre, tu dis :
Notons par t le temps linéaire (où le Big Bang est à t = 0). Notons par to le temps présent (to = 13.7E9 années linéaires).
Posons y = f(t) = a + bln(t), la fonction logarithmique (translatée) qui est tangente à la droite t = t au point t = to.
ln désigne le logarithme naturel (base e).
Dans le voisinage de t = to, les deux échelles se confondent, comme on peut le voir sur le diagramme suivant :
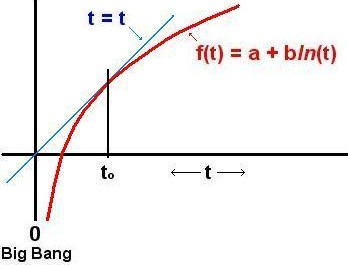
Pour avoir f(to) = to , il faut prendre a et b tels que :
(*) a + bln(to) = to
Pour que la pente (i.e. la dérivée) de f(t) soit 1 (i.e. la pente de t = t) quand t = to, il faut prendre a et b tels que :
(**) f'(to) = b/to = 1
Résolvant les deux équations (*) et (**), on obtient :
b = to et a = to(1 - ln(to))
Substituant ces valeurs dans la définition de f(t), on obtient la forme close :
f(t) = to(1 + ln(t/to))
Selon cette échelle logarithmique, le temps linéaire to = 13.7E9 correspond au temps logarithmique 13.7E9 et le temps linéaire 0 (l'instant du Big Bang) correspond au temps logarithmique "moins l'infini".
Les deux échelles étant équivalentes dans le voisinage de notre présent, c'est pas de la tarte de les distinguer expérimentalement.
Comment savoir laquelle est la "vraie" ?
Maintenant, j'estime qu'il serait "fair play" que tu répondes enfin à mes vieilles questions :
Selon toi, la cause du Big Bang écoute-t-elle nos prières? Juge-t-elle les âmes défuntes?
Ai-je tort d'estimer que ça serait "fair play" que tu y répondes enfin ?
 Denis
Denis
Merci pour ta réponse. Mieux vaut tard que jamais.
Tu dis :
Effectivement, c'est une grandeur sans dimension, comme les décibels.Voici de nouveau mes questions :
Science Création a écrit : Est-ce une grandeur sans dimension comme par exemple l’échelle de magnitude du moment?Ton - ∞ correspond à quel valeur ou domaine de valeur dans l’échelle linéaire ?Science Création a écrit : […] quel est la fonction que tu as en tête qui passe de l'échelle linéaire à l’autre ?
Si on tient à donner un nom à ses unités, on n'a qu'à leur en donner un, comme on fait pour les décibels.
Pourquoi pas des "ères logarithmiques", ou des "années logarithmiques", dans le cas où on ajuste les paramètres de telle sorte que les deux échelles se confondent dans le voisinage de maintenant.
À propos de la fonction qui passe de l'échelle linéaire à l'autre, tu dis :
Tu l'auras voulu :C’est pourtant ce qui est demandé.Denis a écrit : Je n'entre pas dans les détails techniques.
Notons par t le temps linéaire (où le Big Bang est à t = 0). Notons par to le temps présent (to = 13.7E9 années linéaires).
Posons y = f(t) = a + bln(t), la fonction logarithmique (translatée) qui est tangente à la droite t = t au point t = to.
ln désigne le logarithme naturel (base e).
Dans le voisinage de t = to, les deux échelles se confondent, comme on peut le voir sur le diagramme suivant :

Pour avoir f(to) = to , il faut prendre a et b tels que :
(*) a + bln(to) = to
Pour que la pente (i.e. la dérivée) de f(t) soit 1 (i.e. la pente de t = t) quand t = to, il faut prendre a et b tels que :
(**) f'(to) = b/to = 1
Résolvant les deux équations (*) et (**), on obtient :
b = to et a = to(1 - ln(to))
Substituant ces valeurs dans la définition de f(t), on obtient la forme close :
f(t) = to(1 + ln(t/to))
Selon cette échelle logarithmique, le temps linéaire to = 13.7E9 correspond au temps logarithmique 13.7E9 et le temps linéaire 0 (l'instant du Big Bang) correspond au temps logarithmique "moins l'infini".
Les deux échelles étant équivalentes dans le voisinage de notre présent, c'est pas de la tarte de les distinguer expérimentalement.
Comment savoir laquelle est la "vraie" ?
Maintenant, j'estime qu'il serait "fair play" que tu répondes enfin à mes vieilles questions :
Selon toi, la cause du Big Bang écoute-t-elle nos prières? Juge-t-elle les âmes défuntes?
Ai-je tort d'estimer que ça serait "fair play" que tu y répondes enfin ?