C'est loin d'être un record
Publié : 21 mai 2018, 21:15
Treize pieds, ça n'a rien de spectaculaire.
Il y en a qui atteignent presque 200 pieds.
https://fr.wikipedia.org/wiki/Ver_lacet
Treize pieds, ça n'a rien de spectaculaire.
Que croire quelque chose implique qu'on le sait ?Exaptator a écrit : 21 mai 2018, 19:34 Bien réponds toi aussi à la question que j'ai posée à Cadenas.
Pourtant tu dis :Exaptator a écrit : 21 mai 2018, 19:34 Je ne les considère pas vraies en même temps, puisque je les disjoints.
Elles ne sont donc pas vraies en même temps ?Conclusion : je maintiens comme vraies les trois propositions en question :
¬P(¬x) <≠> P(x)
P(x) => ¬P(¬x)
¬P(¬x) ≠> P(x)
Oui.Tu es de mauvaise foi.
Ok, maintenant, si tu es d'accord avec le fait que croire une chose n'implique pas de la savoir, ce qui revient à : C(x) ≠> S(x) ou également à ¬S(x) ≠> ¬C(x), alors tu reconnaîtras que cette vérité ne nous départage pas, mais que c'est exclusivement sur cette vérité, la plus évidente, que tu te bases, n'est-ce pas ?Etienne Beauman a écrit : 21 mai 2018, 22:11Que croire quelque chose implique qu'on le sait ?Exaptator a écrit : 21 mai 2018, 19:34 Bien réponds toi aussi à la question que j'ai posée à Cadenas.
Euh ... non.
Il ne suffit pas d'affirmer une chose pour que ce soit vrai. Donc épouvantail toi-même.Etienne Beauman a écrit : 21 mai 2018, 22:11 ...c'est la déf de croire : tenir pour vrai qui t'amènes à créer cet épouvantail ?
J'ai déjà répondu plus haut :Etienne Beauman a écrit : 21 mai 2018, 22:11Pourtant tu dis :Exaptator a écrit : 21 mai 2018, 19:34 Je ne les considère pas vraies en même temps, puisque je les disjoints.Elles ne sont donc pas vraies en même temps ?Conclusion : je maintiens comme vraies les trois propositions en question :
¬P(¬x) <≠> P(x)
P(x) => ¬P(¬x)
¬P(¬x) ≠> P(x)
Comment ça marche ?
Alternance en fonction des cycles de la lune ?
Oui, dans l'exemple que tu donnes certaines propositions sont fausses mais indépendamment des autres. Dans mon exemple ce n'est pas tout-à-fait comme ça.Etienne Beauman a écrit : 21 mai 2018, 22:11 Est ce que tu captes au moins, qu'avec ce mode de "logique" tu peux dire strictement n'importe quoi ?
Je déclares vraie :
les poules ont des dents
Michael Jackson est vivant
les camions sont bleus
L'homme est un mammifère
si je mets des ou entre chaque phrase, comme la dernière est vrai l'ensemble est vrai, en revanche les phrases 1 à 3 ne sont pas vraies est on au moins d'accord là dessus ?
J'ai déjà répondu plus de trois fois à ces objections et à chaque fois en expliquant différemment, et tu me ressers toujours la même salade...Etienne Beauman a écrit : 21 mai 2018, 22:11 Si tes propositions étaient vraies, elles pourraient l'être en même temps.
Quand est ce que tu vas percuter ?
p : a est vrai ou non a est vrai
p est toujours vrai, mais l'une des deux alternatives est nécessairement fausse, foutu principe de non contradiction !
Réveille toi, tu fais de la logique mystique.
C'est bien de le reconnaître !
Les vérités générales sont assez souvent conditionnelles, - et c'est le moins que l'on puisse dire ! -, le nies-tu ?Etienne Beauman a écrit : 21 mai 2018, 22:11 Et toi tu vis dans un monde où des vérités générales peuvent être fausse quand ça t'arrange.
Non non non !Exaptator a écrit : 22 mai 2018, 18:38 Ok, maintenant, si tu es d'accord avec le fait que croire une chose n'implique pas de la savoir, ce qui revient à : C(x) ≠> S(x)
___________________________Conclusion : je maintiens comme vraies les trois propositions en question :
¬P(¬x) <≠> P(x)
P(x) => ¬P(¬x)
¬P(¬x) ≠> P(x)
Pétition de principe, tu démontres que le savoir n'est pas une croyance car le savoir n'est pas une croyance.Affirmer que savoir est une sorte de croyance est une absurdité, car quand on croit une chose, cela revient à ne pas la savoir, car sinon on la saurait, autrement dit : on serait dans ce cas en mesure de la prouver.
Non.Ce que tu soutiens c'est ceci
Si c'est l'affirmation d'une possibilité, pourquoi ne dis tu pas possible à la place de vraie ?Exaptator a écrit : 22 mai 2018, 18:38 Une affirmation disjointe est l'affirmation de la possibilité
Si tes propositions sont alternativement vraies et fausse (forcément) pourquoi écris tu qu'elles sont vraies ?Mes propositions sont alternativement vraies selon les cas.
Oui, une vérité générale est une propositions convenue comme vraie (truisme) dans le cadre où elle s'applique, si tu énonces des trucs pouvant être vrai ou faux dans le cadre de leur utilisation ce ne sont de toutes évidence pas des vérités générales.Les vérités générales sont assez souvent conditionnelles, - et c'est le moins que l'on puisse dire ! -, le nies-tu ?
On s efiche de l'absolu.Des vérités générales vraies dans l'absolu
Etienne Beauman a écrit : 22 mai 2018, 21:31Non non non !Exaptator a écrit : 22 mai 2018, 18:38 Ok, maintenant, si tu es d'accord avec le fait que croire une chose n'implique pas de la savoir, ce qui revient à : C(x) ≠> S(x)
L'absence d'implication ne revient pas à une non-implication.
Etienne Beauman a écrit : 22 mai 2018, 21:31 S = a ∧ b
Est ce que a-> S ?
non.
Est ce que a ≠> S ?
non plus.
Raisonne sérieusement ou ne le fais pas.
Il me fait marrer ton x nu. Explique moi formellement comment tu en détermines la vérité. J'ai hâte de lire ta réponse...
Etienne Beauman a écrit : 22 mai 2018, 21:31 Je n'affirme pas T(x)->S(x) et je n'affirme pas T(x) ≠> S(x)
Etienne Beauman a écrit : 22 mai 2018, 21:31 Tu ne sembles toujours pas comprendre comment ça marche, les implications doivent pouvoir se déduire du tableau de vérité.
Etienne Beauman a écrit : 22 mai 2018, 21:31 J'attends d'ailleurs toujours tes démonstrations...
x_T(x)_J(x)_S(x)
0__0____0___0
0__0____1___0
0__1____0___0
0__1____1___0
1__0____0___0
1__0____1___0
1__1____0___0
1__1____1___1
Etienne Beauman a écrit : 22 mai 2018, 21:31 Par exemple, à chaque fois* que S(x) vaut 1, x vaut 1, et quand S(x) vaut 0, on voit que x peut valoir soit 1 soit 0, les deux conditions de la relation d'implication sont vérifiées, donc S(x)->x.
Etienne Beauman a écrit : 22 mai 2018, 21:31 On l'a sort pas de nulle part, on la lit dans le tableau.
Et on peut l'écrire dans un nouveau tableau
x_S(x)_S(x)->x
0_0______1
0_1______0
1_0______1
1_1______1
Et comme le cas où S(x)->x est faux ne se trouve pas dans notre tableau initiale, on peut vérifier que S(x)->x est toujours vraie
Etienne Beauman a écrit : 22 mai 2018, 21:31 Marrant mes affirmations à moi, elles sont toujours vraies en même temps sans souci.
Etienne Beauman a écrit : 22 mai 2018, 21:31 Si T(x) ≠> S(x), à chaque fois que T(x) vaut 1 dans le tableau, S(x) devrait valoir 0.
Est ce que c'est le cas ?
Non, ça suffit pour dire qu'il n'y a pas de non-implication.
Etienne Beauman a écrit : 22 mai 2018, 21:31 Mais le pire, c'est que si T(x) ≠> S(x) était vraie et non pas possible, T(x) devrait toujours valoir 1 ! **
Etienne Beauman a écrit : 22 mai 2018, 21:31 Le seul cas qui invaliderait l'implication S(x)->x, c'est S(x)∧¬x, est ce que tu le voie dans le tableau ?
Non.
Etienne Beauman a écrit : 22 mai 2018, 21:31 Les 3 cas qui invalident T(x) ≠> S(x) sont ¬T(x)∧S(x), ¬T(x)∧¬S(x) et T(x)¬S(x), je les ai mis en rouge.
S'il y a des erreurs dans ce que j'ai énoncé, tu ne les as pas montrées.Etienne Beauman a écrit : 22 mai 2018, 21:31 Encore une fois depuis des semaines, t'as tout ce qu'il faut pour comprendre ton erreur, il faut juste que tu comprennes qu'on décrètes pas des implications ou des non-implications, on les déduits du tableau de vérité.
Etienne Beauman a écrit : 22 mai 2018, 21:31Exaptator a écrit : 22 mai 2018, 18:38 Affirmer que savoir est une sorte de croyance est une absurdité, car quand on croit une chose, celarevient à[implique de] ne pas la savoir, car sinon on la saurait, autrement dit : on serait dans ce cas en mesure de la prouver.
Pétition de principe, tu démontres que le savoir n'est pas une croyance car le savoir n'est pas une croyance.
Etienne Beauman a écrit : 22 mai 2018, 21:31Non.
Réponds à ce que je dis, pas à des positions imaginaires
Ce que je dis c'est S(x) = x∧T(x)∧J(x)
Rien d'autre.
Etienne Beauman a écrit : 28 mars 2018, 10:14 Si non,
Quelle est donc ta définition de savoir, et pourquoi ne pas utiliser La définition de la connaissance communément utilisée en épistémologie ( connaissance = croyance vraie justifiée ; Con(x) = x . T(x) . P(x) ?
Etienne Beauman a écrit : 28 mars 2018, 15:58Exaptator a écrit : En effet, si c'était une croyance, savoir ne serait pas distinguable de croire, ce qui poserait quelques problèmes de nature dialectique. Et aussi, parler de preuve n'aurait aucun sens dans ce cas...
Faux.
On peut distinguer croyance et connaissance.
Une connaissance est un type particulier de croyance, tout comme les lapins est un type particulier de mammifères, une connaissance est une croyance vraie justifiée, la notion de preuve y joue un rôle tout comme la vérité en elle même de la proposition ( le risque d'erreur n'est pas écarté d'un revers de main).
Etienne Beauman a écrit : 22 mai 2018, 21:31Si c'est l'affirmation d'une possibilité, pourquoi ne dis tu pas possible à la place de vraie ?Exaptator a écrit : 22 mai 2018, 18:38 Une affirmation disjointe est l'affirmation de la possibilité
Mes propositions ne sont pas alternativement vraies et fausses, mais vraies ou fausses.Etienne Beauman a écrit : 22 mai 2018, 21:31Exaptator a écrit : Mes propositions sont alternativement vraies selon les cas.
Si tes propositions sont alternativement vraies et fausse (forcément) pourquoi écris tu qu'elles sont vraies ?
Etienne Beauman a écrit : 22 mai 2018, 21:31Oui, une vérité générale est une propositions convenue comme vraie (truisme) dans le cadre où elle s'applique, si tu énonces des trucs pouvant être vrai ou faux dans le cadre de leur utilisation ce ne sont de toutes évidence pas des vérités générales.Exaptator a écrit :Les vérités générales sont assez souvent conditionnelles, - et c'est le moins que l'on puisse dire ! -, le nies-tu ?
La lune en mousse qui me sert parfois d'oreiller invalide ton propos.Etienne Beauman a écrit : 22 mai 2018, 21:31On s efiche de l'absolu.Exaptator a écrit :Des vérités générales vraies dans l'absolu
La lune n'est pas en mousse est une vérité générale pour le commun des mortels pas complétement zinzins, sur ce forum de discussion personne de censé ne viendra la contredire.
Il va falloir argumenter au moins un cran au dessus
Et alors ?- Il n'y a pas de "=" en logique classique formelle.
Etienne Beauman a écrit : 27 mai 2018, 19:53
Mais boubours, dans l'exemple S= a.b, a et b sont deux variables indépendantes.
C'est au dessus de mes forces, tu comprends même pas le principe de système logique.
Et tu voudrais faire croire que je ne le saurais pas ou que je confondrais (a => b) et (a ∧ b) ?Etienne Beauman a écrit : 27 mai 2018, 19:53Et alors ?- Il n'y a pas de "=" en logique classique formelle.
Quand on fait de la logique numérique, tu sais avec des 0 et des 1, on pratique l'algèbre de boole.
Il faudrait que tu t'y interesses un de ses quatre, tu comprendrais peut être qu'on distingue les entrées des sorties, et que a->b et à.b sont l'expression de deux systèmes différents, pas contraires différents, qu'on peut même simuler physiquement.
Fais moi passer pour un idiot et nos lecteurs avec tant que tu y es !Etienne Beauman a écrit : 27 mai 2018, 19:53 A et B sont les entrées, S est la sortie, le système S=a.b est une égalité entre la relation logique des variables d'entrée et la valeur de la sortie.
Quand on crée le système S= a.b, il n'y a ni relation d'implication entre a et b, ni relation de non-implication entre a et b. , a et b sont des variables independantes.
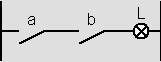
Physiquement S peut être une lampe et à et b deux interrupteurs indépendants. .
S vaut L ici
Si tu veux simuler S'= a->b ou S''= a≠>b tu dois faire des montages différents.
Oui et ? Est-ce que j'aurais dit le contraire ?Etienne Beauman a écrit : 27 mai 2018, 19:53 En revanche S -> a, tout comme S ->b, est vraie, tout le temps, l'implication est réelle.
On peut la déduire formellement,
(S<->a∧b)->(S->a∧S->b)
Tu rêves.Exaptator a écrit : 27 mai 2018, 21:49 Dit le gars qui ne s'était pas rendu compte qu'il affirmait en même temps p ∧ ¬p
Oh non je ne rêve pas ! Il suffit de te relire.Etienne Beauman a écrit : 27 mai 2018, 23:09Tu rêves.Exaptator a écrit : 27 mai 2018, 21:49 Dit le gars qui ne s'était pas rendu compte qu'il affirmait en même temps p ∧ ¬p
Quand j'affirme s= a.b , je n'affirme rien d'autre.
Je n'affirme pas a-->b, signifie que je ne fais pas cette affirmation, ça ne signifie pas que j'affirme le contraire.
Etienne Beauman a écrit : 22 mai 2018, 21:31Non non non !Exaptator a écrit : 22 mai 2018, 18:38 Ok, maintenant, si tu es d'accord avec le fait que croire une chose n'implique pas de la savoir, ce qui revient à : C(x) ≠> S(x)
L'absence d'implication ne revient pas à une non-implication.
Etienne Beauman a écrit : 22 mai 2018, 21:31 S = a ∧ b
Est ce que a-> S ?
non.
Est ce que a ≠> S ?
non plus.
Mais bon... Si tu n'as pas compris les première fois... , je crains que rien ne puisse te sortir de ta présomption égotique, et surtout pas la raison.Exaptator a écrit : 27 mai 2018, 16:45Ah mais fallait le dire tout de suite que tu doutes du principe du tiers exclu !








SpoilerAfficherEt pourquoi (a => (a ∧ b)) devrait-elle fausse, étant donné que (a => (a ∧ b)) <=> ((a => b)) ?
En effet, si (a => b) est vraie, alors (a => (a ∧ b)) est nécessairement vraie.
De même, pourquoi (a ≠> (a ∧ b)) devrait-elle fausse, étant donné que (a ≠> b) <=> (a ≠> (a ∧ b)) ?
En effet, si (a ≠> b) est vraie, alors (a => (a ∧ b)) est nécessairement fausse, autrement dit :
Si (a ≠> b) est vraie, alors (a ≠> (a ∧ b)) est nécessairement vraie.
Donc en fait, ce que tu dis c'est que tu ne sais pas si (a => b) ou bien si (a ≠> b) ce que je pourrais passer, ou pire mais là c'est absurde, tu dis implicitement que tu doutes que (a => b) ∨ (a ≠> b) => ⊤, ou encore, et là y a pas plus pire : tu dis que ¬(a => (a ∧ b)) et que ¬(a ≠> (a ∧ b)) !
_ E.B. : T(¬ (a => (a ∧ b))) ∧ ¬ (a ≠> (a ∧ b)))________
_________0_1_1_ 1_1_1 _ 0_1_1_0__1_1_1_________
_________1_1_0_ 1_0_0 _ 0_0_1_1__1_0_0_________
_________0_0_1_ 0_0_1 _ 0_1_0_0__0_0_1_________
_________0_0_1_ 0_0_0 _ 0_1_0_0__0_0_0_________
>>>>>>>>>>>>>>>>>>>>>


En effet, en logique classique on a : (a => b) ∨ (a ≠> b) => ⊤
________(a => b) ∨ (a ≠> b)_________
________ 1_1_1_ 1_1_0_ 1__________
________ 1_0_0_ 1_1_1_ 0__________
________ 0_1_1_ 1_0_0_ 1__________
________ 0_1_0_ 1_0_0_ 0__________
Donc pour en revenir à ce dont il était question, - moi je fais les liens -, ce que tu dis c'est au mieux, en étant gentil en tordant un peu à ton avantage pour alléger le ridicule :
E.B. : ¬S(C(x) => S(x)) ∧ ¬S(C(x) ≠> S(x))
<=> E.B. : ¬S((C(x) => S(x)) ∨ (C(x) ≠> S(x))
<=> E.B. : ¬S(p ∨ ¬p)
>>>>>>>>>>>>>>>>>>>>>>>> Le ridicule ne tue pas...... ()
Ou au pire, mais c'est là exactement ce que tu écris :
E.B. : T(¬(C(x) => S(x)) ∧ ¬(C(x) ≠> S(x))
<=> E.B. : T((C(x) ≠> S(x)) ∧ (C(x) => S(x))
<=> E.B. : T(p ∧ ¬p)
>>>>>>>>>>>>>>>>>>>>>>> Mais à ce point je me demande toutefois si cela ne serait pas dangereux pour la rate.
Mes côtes me font mal.... (

)
Remarques :
- Il n'y a pas de "=" en logique classique formelle.
- Je ne vois pas en ces lignes le moindre argument pouvant me contredire.
- Tu ne montres pas les liens qu'il y aurait avec ce que j'ai dit.
Apprends donc déjà à formaliser proprement et après on discutera peut-être sérieusement si tu en es capable.
Moi j'appelle ça de l'imposture, de la diversion et du noyage de poisson ou plus simplement, mais c'est alors une autre histoire : de l'incapacité à raisonner correctement.
Ah mais quelle tarte tu fais !Etienne Beauman a écrit : 27 mai 2018, 23:09 Dans le système s=a.b il n'y a qu'une relation logique entre a et b, ce n'est ni une implication, ni une non-implication, c'est une conjonction.
Tu parles maintenant d'équivalence....Etienne Beauman a écrit : 27 mai 2018, 23:09 P1 : le prochain pape sera belge.
P2 : le prochain acteur incarnant James bond sera noir.
Oserai tu affirmer p1<->p2 ?
Ah parce que tu n'affirmerais jamais des choses fausses au point d'être ridicule ?Etienne Beauman a écrit : 27 mai 2018, 23:09 et arrête ton cinéma j'entends par là affirmer vrai (désolé du pleonasme), affirmer des choses fausses pour tenir des raisonnements contradictoires ne m'intéresse pas.
Ah mais bon... ton avis sur ce qui serait pertinent ou "à deux balles" étant celui d'un gugusse qui rejette la logique classique dans sa cohérence, le donner ou te le garder revient au même.Etienne Beauman a écrit : 27 mai 2018, 23:09 Selon ta logique a deux balles, Soit tu réponds oui et ta justification sera absurde, soit tu réponds non et ça voudrait dire que tu affirmés que p1<≠>p2, et ta justification sera absurde.
Alors qu'il n'y a juste aucune raison d'affirmer que ces deux propositions sont reliés par une quelvonque relation logique.
Lol ! Absence de relation..... En logique classique.... lol, lol et re lol.Etienne Beauman a écrit : 27 mai 2018, 23:09 Il y a quatre cas, tous possibles, ---> absence de relation.
Constater une absence de relation ne signifie pas affirmer.les relations contraires à toutes celles qu'on affirme pas.
Pas entre les même termes !Exaptator a écrit : 28 mai 2018, 13:29 s-tu pas qu'une conjonction est toujours strictement équivalente à une non-implication :
Épouvantail, tu me fais affirmer des choses quand je t'indique que je ne les affirme pas.Exaptator a écrit : 28 mai 2018, 13:29 Moi ce qui est sûr c'est que je n'affirmerai pas à ta manière des choses comme :
(P1 => P2) ∧ (P1 ≠> P2) ou comme ¬(P1 => P2) ∧ ¬(P1 ≠> P2).....
HS,Exaptator a écrit : 28 mai 2018, 13:29 Et tu dis encore n'importe quoi, (a ∧ b) ce n'est pas aucune relation logique, c'est une conjonction.
Bien oui, mais ça c'est une évidence ho !Etienne Beauman a écrit : 28 mai 2018, 14:51Pas entre les même termes !Exaptator a écrit : 28 mai 2018, 13:29 Ne sais-tu pas qu'une conjonction est toujours strictement équivalente à une non-implication :
Une conjonction entre deux termes est équivalente à une non-implication entre l'un des termes et la négation de l'autre.
Bien sûr, puisque le lien logique entre a et b est une conjonction, autrement dit un "∧".Etienne Beauman a écrit : 28 mai 2018, 14:51 Relis moi, il n'y a ni implication entre a et b, ni non-implication entre a et b.
Donc essaye d'être un tout petit peu conséquent si tu en es capable, car je le regrette, mais le "∧" est une relation logique comme une autre. Qui peut donc être vraie ou fausse en logique classique.Etienne Beauman a écrit : 27 mai 2018, 23:09 ...il n'y a juste aucune raison d'affirmer que ces deux propositions sont reliés par une quelvonque relation logique.
Oui donc si (a ∧ b) est vraie, alors il est également vrai que (a ≠> ¬b), donc ça je l'affirme, c'est une non implication qui lie a et ¬b par la conjonction qui lie a et b, b et ¬b étant contradictoires, et puisque je suis conséquent dans ce que je dis, j'exclus le fait que a impliquerait b, je le répète : si (a ∧ b) est vraie.Etienne Beauman a écrit : 27 mai 2018, 23:09 Relis toi, ce que t'as trouvé c'est une non-implication entre a et non b.
C'est un premier point.
(J'ai mis en gros.)Etienne Beauman a écrit : 22 mai 2018, 21:31 L'absence d'implication ne revient pas à une non-implication.
Etienne Beauman a écrit : 22 mai 2018, 21:31 S = a ∧ b
Est ce que a-> S ?
non.
Est ce que a ≠> S ?
non plus.
Oui, ((a ∧ b) => a) est ce qu'on appelle une tautologie. C'est comme (a ∨ ¬a) => ⊤ ou comme je l'ai écrit plus haut, c'est comme : (a => b) ∨ (a ≠> b) => ⊤ que tu niais.Etienne Beauman a écrit : 28 mai 2018, 14:51 De plus on a bien
S = (a ∧ b) ) <=> (a ≠> ¬b)
On a pas
a ≠> ¬b
Ça ça peut être faux, contrairement à S->a qui est toujours vrai.
Bien sûr que l'on peut affirmer (a ≠> ¬b) si (a ∧ b) est établie, et si ce n'est pas le cas on peut toujours l'affirmer disjonctivement avec les autres cas possibles... Je ne vois pas ce qui pose problème...Etienne Beauman a écrit : 28 mai 2018, 14:51 Je peux affirmer S->a. C'est une déduction tautologique du système.
Je ne peux pas affirmer a ≠> ¬b, ce n'est qu'un cas possible sur quatre, a et b sont des variables independantes.
Absolument pas ! Je reprends exactement ce que tu as écrit.Etienne Beauman a écrit : 28 mai 2018, 14:51Épouvantail, tu me fais affirmer des choses quand je t'indique que je ne les affirme pas.Exaptator a écrit : 28 mai 2018, 13:29 Moi ce qui est sûr c'est que je n'affirmerai pas à ta manière des choses comme :
(P1 => P2) ∧ (P1 ≠> P2) ou comme ¬(P1 => P2) ∧ ¬(P1 ≠> P2).....
Etienne Beauman a écrit : 22 mai 2018, 21:31 S = a ∧ b
Est ce que a-> S ?
non.
Est ce que a ≠> S ?
non plus.
Où t'as vu que je me défilais, est-ce mon habitude ? Je réponds point par point à quasiment 100 % de mes interventions.Etienne Beauman a écrit : 22 mai 2018, 21:31 Mais sinon tu te défiles, il y a t il une relation d'équivalence, oui ou non, entre P1 et P2 ?
Bien tu soutenais le contraire..... Ce n'est jamais HS de relever une erreur dans un discours.Etienne Beauman a écrit : 28 mai 2018, 14:51HS,Exaptator a écrit : 28 mai 2018, 13:29 Et tu dis encore n'importe quoi, (a ∧ b) ce n'est pas "aucune relation" logique, c'est une conjonction.
Ah bon ? Tu sais ce qui est vrai avant de raisonner dessus ? T'es fort toi....Etienne Beauman a écrit : 28 mai 2018, 14:51 Dernier point, dans un raisonnement par l'absurde on sait parfaitement que la proposions qu'on considère vrai, ne l'est pas, c'est ce qu'on veut démontrer.
On affirme pas p, on fait comme si p, et on trouve une contradiction, et on en conclus non p
L'affirmation c'est la conclusion, pas la prémisse.
Oh Putain on l'a perdu.Exaptator a écrit : 28 mai 2018, 20:38 Donc essaye d'être un tout petit peu conséquent si tu en es capable,
Non mais tu te fous de la G du monde. Tu ne reconnais jamais tes âneries ?Etienne Beauman a écrit : 28 mai 2018, 21:05Oh Putain on l'a perdu.Exaptator a écrit : 28 mai 2018, 20:38 Donc essaye d'être un tout petit peu conséquent si tu en es capable,
Cette citation concerne p1 et p2 pas a et b.
Relis calmement les messages précédent, et revient avec des arguments qui concernent ce que je dis et pas autre chose.
Comment ça sinon ? Tu ne fais que ça.
Si tu appelles te troller, montrer tes incohérences, je comprends que tu n'aimes pas forcément, mais un troll ce n'est pas ça, c'est plutôt quelqu'un qui te ressemble.Etienne Beauman a écrit : 28 mai 2018, 21:05 Si tu veux me troller il faut que ce soit un minimum intéressant pour moi. Là, c'est trop débile.
Les deux propositions en question sont p1 et p2, si tu n'as pas l'honnêteté intellectuelle de le reconnaître, c'est ton problème.
P1 : le prochain pape sera belge.
P2 : le prochain acteur incarnant James bond sera noir.
Oserai tu affirmer p1<->p2 ?
et arrête ton cinéma j'entends par là affirmer vrai (désolé du pleonasme), affirmer des choses fausses pour tenir des raisonnements contradictoires ne m'intéresse pas.
Selon ta logique a deux balles, Soit tu réponds oui et ta justification sera absurde, soit tu réponds non et ça voudrait dire que tu affirmés que p1<≠>p2, et ta justification sera absurde.
Alors qu'il n'y a juste aucune raison d'affirmer que ces deux propositions sont reliés par une quelvonque relation logique.
Il y a quatre cas, tous possibles, ---> absence de relation.
Alors quand tu me repondsDans le système s=a.b il n'y a qu'une relation logique entre a et b, ce n'est ni une implication, ni une non-implication, c'est une conjonction.
Tu me parles d’honnêteté intellectuelle ? Toi ?Etienne Beauman a écrit : 28 mai 2018, 23:38 Les deux propositions en question sont p1 et p2, si tu n'as pas l'honnêteté intellectuelle de le reconnaître, c'est ton problème.
T'es sûr ? Moi je dirais plutôt ce n'est pas ma faute si t'es inconséquent...
(J'ai mis en gros.)Etienne Beauman a écrit : 22 mai 2018, 21:31 L'absence d'implication ne revient pas à une non-implication.
Etienne Beauman a écrit : 22 mai 2018, 21:31 S = a ∧ b
Est ce que a-> S ?
non.
Est ce que a ≠> S ?
non plus.
Etienne Beauman a écrit : 22 mai 2018, 21:31 S = a ∧ b
Est ce que a-> S ?
non.
Est ce que a ≠> S ?
non plus.
Ah bon ? Tu sais ce qui est vrai avant de raisonner dessus ? T'es fort toi....Etienne Beauman a écrit : 28 mai 2018, 14:51 Dernier point, dans un raisonnement par l'absurde on sait parfaitement que la proposions qu'on considère vrai, ne l'est pas, c'est ce qu'on veut démontrer.
On affirme pas p, on fait comme si p, et on trouve une contradiction, et on en conclus non p
L'affirmation c'est la conclusion, pas la prémisse.
J'ai déjà répondu :Etienne Beauman a écrit : 28 mai 2018, 23:38 Soit tu réponds oui et ta justification sera absurde, soit tu réponds non et ça voudrait dire que tu affirmés que p1<≠>p2, et ta justification sera absurde.
Alors qu'il n'y a juste aucune raison d'affirmer que ces deux propositions sont reliés par une quelvonque relation logique.
Exaptator a écrit : 28 mai 2018, 20:38 Réponse :
Je n'en sais rien : Exaptator : ¬S((P1 => P2) ∧ (P2 => P1))
En tout cas je ne l'affirme pas : Exaptator : ¬T((P1 => P2) ∧ (P2 => P1))
Tes P1 et P2 sont des propositions assertives. Si tu les affirmes tu dois les mettre en lien, sinon tu ne les affirmes pas.Etienne Beauman a écrit : 28 mai 2018, 23:38 Il y a quatre cas, tous possibles, ---> absence de relation.
Oui et je persiste.
Tu disais, je te cites :
Etienne Beauman a écrit : ↑22 mai 2018, 20:31
L'absence d'implication ne revient pas à une non-implication.
L'étranger a écrit :Comme dirait quelqu’un de beaucoup plus avisé que moi : quelque fois c’est toi qui cogne le bar, mais d'autres fois, et ben, c'est le bar qui te cogne.
Eh bien tu persistes dans l'erreur et dans l’imbécillité de tes propos, car deux propositions assertives, prenons a et b qui ne seraient données sans relation logique ne sont tout bonnement pas des propositions logiques.Etienne Beauman a écrit : 31 mai 2018, 10:34Oui et je persiste.Exaptator a écrit :Tu disais, je te cites :
Etienne Beauman a écrit : ↑22 mai 2018, 20:31
L'absence d'implication ne revient pas à une non-implication.
Et dans ce cas il y a une non implication..... T'as du mal.....Etienne Beauman a écrit : 31 mai 2018, 10:34 Si entre deux propositions, le lien logique n'est pas une implication, alors il n'y a pas d'implication entre ces deux propositions.....
Etienne Beauman a écrit : ↑22 mai 2018, 20:31Etienne Beauman a écrit : 31 mai 2018, 10:34 Ça ne veut pas dire qu'il y a nécessairement une non-implication entre ces deux propositions.
Ah mais la logique cher ami c'est tout ce qu'il y a de plus binaire. Si tu as mieux à proposer je t'écoute.Etienne Beauman a écrit : 31 mai 2018, 10:34 Tu réduis la relation entre deux propositions à une alternative binaire, c'est absurde.
---------> Voilà qu'il remet une couche à ses couches....Etienne Beauman a écrit : 31 mai 2018, 10:34 C'est probablement une conséquence direct de ton obstination à vouloir définir en utilisant des équivalences plutôt que des égalités.