Excellentes réponses, bon, on ne va pas s'éterniser la dessus, faut pas oublier qu'à l'origine on devait tous être capable de résoudre ça dès nos 12 ou 13 ans...
réponse:
de 6h40 à 8h40 le train A a parcouru 2 * 143 = 286 km
il reste aux deux trains à parcourir 967 - 286 = 681 km
L'astuce est de considérer que B reste immobile pendant que A parcourt cette distance:
Le trajet restant serait donc réalisé en reportant la vitesse de chacun sur l'autre train, soit:
le train A ferait donc le trajet en 681 km / (143 + 193)km/h = 2.027 heures à la vitesse de 336 km/h
et le croisement serait forcément à Marseille...
Cela posé, on connait la date du croisement donc on revient maintenant aux conditions réelles.
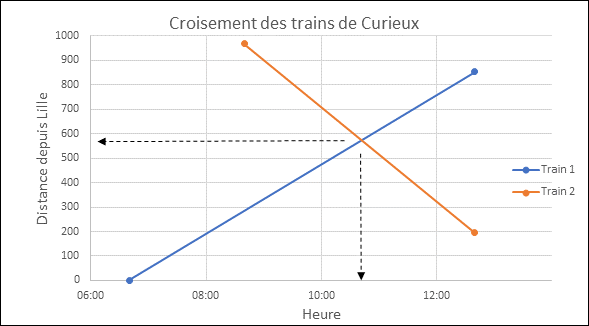
1- 8h40 + 2.027h = 10h41mn36s
2- 286 km + (143 * 2.027) = 286 + 289.861 km = à 575.8 km de Lille
3- 193 * 2.027 = à 391.2 km de MARSEILLE
Verif : 575.8 + 391.2 = 967 km
méthode algébrique:
967 - (2 * 143) = x * 143 + y * 193)
x, homogène à un temps étant forcément égale à y, c'est un croisement, l'équation n'a qu'une inconnue (*).
967 - (2 * 143) = x * (143 + 193)
0 = (2 * 143) + x * (143 + 193) - 967
0 = 336 * x - 681
x = 681 / 336
x = 2.026785714 heures
(*) avec deux inconnues il faudrait deux expressions sinon c'est tintin :
ax + by = c
et
a'x + b'y = c'
avec ab' - a'b # 0
Ce problème est une expression de la relativité à la mode de Galilée.
Aucun des deux trains ne se considère ni comme immobile ni comme roulant, les vitesses relatives s'ajoutent sans privilégier un train en particulier.
On a choisi de rendre B immobile pour le simplifier mais le problème serait aussi bien résolu en faisant le contraire.
Le croisement aurait alors eu lieu à 283 km de Lille, train A à l’arrêt à cet endroit.
En clair, conformément à la relativité des mouvements rectilignes uniformes, il existe une infinité de solutions pour le lieu du croisement
mais une seule vitesse relative dans le référentiel des deux trains : 143 + 193 = 336 km/h
Pour avoir une seule solution à la distance du croisement il faut un 3eme référentiel, celui de la gare, c'est par rapport à elle que les vitesses 'réelles' sont fixées.
Autrement dit, ce qu'on appelle improprement 'réalité' ne dépend dans ce problème de croisement que du référentiel de la gare.
Référentiel aussi relatif que n'importe quel autre, et si on a mentalement tendance à le prendre comme absolu
c'est uniquement parce qu'on passe le plus clair de notre temps dans celui là.
Une fois ce principe correctement assimilé, il devient clair que le jeune Einstein tenait à résoudre le problème qui le préoccupait :
si je tiens un aimant dans une main et une bobine dans l'autre, pourquoi le galvanomètre relié à la bobine dévie-il quelque soit la main qui bouge en direction de l'autre ?
On connait la suite.
Le rôle de la physique mathématique est de bien poser les questions, ce n'est que l'expérience qui peut les résoudre. [Henri Poincaré]