Sondage et faibles échantillons : réellement représentatif ?

[Alx]

Bonjour à tous !

Petite question qui me trotte dans la tête depuis un moment et j'aurais aimé votre avis par rapport à tous les divers sondages que l'on peut nous présenter dans les médias. En effet, il m'a toujours paru étrange que l'on puisse généraliser à une population de plusieurs dizaines de millions de personnes le résultat d'un simple sondage effectué sur un échantillon de, par exemple, seulement 1000 - 1500 personnes (il me semble que c'est la fourchette communément utilisée non ?) .

Je sais que cela touche pleinement au domaine des statistiques mais j'aurais aimé savoir dans quelle mesure peut-on faire confiance à de tels sondages pour un échantillons qui me paraît aussi faible.

Si quelqu'un peut m'expliquer, avec méthodes statistiques à l'appui s'il le faut, en quoi un simple échantillon est tout à fait représentatif d'une population entière, je lui serai reconnaissant éternellement !

Merci d'avance !

Alx

[Denis]

Salut Alx,

Tu dis :

il m'a toujours paru étrange que l'on puisse généraliser à une population de plusieurs dizaines de millions de personnes le résultat d'un simple sondage effectué sur un échantillon de, par exemple, seulement 1000 - 1500 personnes.
(...)
Si quelqu'un peut m'expliquer, avec méthodes statistiques à l'appui s'il le faut, en quoi un simple échantillon est tout à fait représentatif d'une population entière, je lui serai reconnaissant éternellement !

Je ne sais pas à quel point tu souhaites une réponse "forte", qui va jusqu'au bout du bout de tous les détails des détails.

Je vais me contenter de commenter le tableau suivant



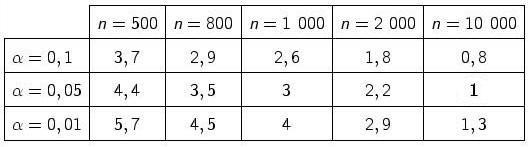
qu'on trouve au bas de cette page sur l'estimation d'une proportion (inconnue) p, dans une grande population de taille N.

Cette proportion p est estimée (i.e. approximée numériquement) par la fréquence f observée dans un échantillon (de taille n) tiré au hasard dans la population. Plus grand l'échantillon, meilleure est la précision.

Les nombres du tableau (où l'on considère que la taille N de la population est infinie) indiquent, pour différents "risques d'erreur" α et différentes tailles d'échantillon n, la précision obtenue (en %) dans le cas le plus défavorable (i.e. quand la véritable valeur (inconnue) de p est voisine de ½).

Quand, dans les médias, on présente les résultats d'un sondage, on ajoute souvent une petite phrase du genre : « la taille (1000) de l'échantillon nous assure que cette estimation est précise à 3% près, 19 fois sur 20 ». C'est le 3 qu'on trouve dans la case du tableau correspondant à α = 5% (i.e. 1 chance sur 20 de se tromper) et n = 1000.

On pourrait aussi dire : « la taille (1000) de l'échantillon nous assure que cette estimation est précise à 4% près, 99 fois sur 100 ».

Je rappelle que, dans le tableau, on suppose que la population est infinie (N = ∞). Si N n'est pas incommensurablement plus grand que n, les intervalles de confiance sont un peu plus étroits. Techniquement, leur rayon est multiplié par (1 - (n/N))½, ce qui ne change pas grand chose tant que la fraction d'échantillonnage n/N est petite. Par exemple, un échantillon de taille 1000 tiré parmi 1.35 milliard de Chinois fournit des estimations pratiquement aussi précises qu'un échantillon de taille 1000 tiré parmi 35000 Liechtensteiniens car, dans les deux cas, les fractions d'échantillonnage (1/1350000 et 1/35) sont petites.

Je ne sais pas à quel point j'ai répondu à ta question. Si j'ai répondu à côté, ne te gênes pas pour le dire. J'essayerai de faire mieux.

Denis

P.S. Pour la reconnaissance éternelle, ne te sens pas obligé.

[Dash]

Moi aussi, il y a quelques années, cette question m'embêtai.

Je vais tenter de vulgariser, ce qu'explique de façon de maitre, Denis.

Ce n'est pas tant le nombre d'échantillons en soi qui est important (bien sûr ça prend un minimum nécessaire), mais la
technique de prélèvement qui doit être fait au hasard de manière à « piger » équitablement dans tous les groupes possible.

« Groupe possible » dans le sens de tous les groupes d'âge, toutes les classes scocial, hommes, femmes, riches, pauvres, etc..

Moi, j'avais saisi avec un exemple en regardant un reportage sur les sondages à la TV :

Dans un grand chaudron de soupe aux légumes, on mélange avec la louche pour s'assurer une dispersion, une répartition
homogène de tous les ingrédients.

Ensuite on prend rapidement, au hasard, un peu de soupe avec la louche.

Résultat : la répartition entre le volume de liquide et le nombre de morceaux de petit pois, de carottes, de céleris et autres
ingrédients serra pratiquement la même que dans le grand chaudron!



Bien sur, comme le mentionne Denis, plus la louche est grande, plus le taux d'erreur diminue, mais le facteur essentiel, c'est que
le prélèvement doit se faire de façon tout à fait hasardeuse en s'assurant de prélever également dans tous les groupes possibles.

Pour l'exemple de la soupe, c'est le fait de bien brasser cette dernière qui assure la répartition. Pour les sondages, c'est la technique
de prélèvement qui s'assure de bien brasser les échantillons disponibles provenant de l'ensemble de la population.

P.S. Moi j'aimerais bien un peu de reconnaissance éphémère.

[Alx]

Merci à tout deux pour ces explications.

C'est plus clair effectivement, même si j'ai un peu oublié les statistiques apprises en prépa..

En fait, c'est effectivement le ciblage de l'échantillon qui semble important dans cette histoire. Mais cela reste pour moi tout à fait contre-intuitif et réducteur de ne prendre que 1000 personnes pour généraliser à toute la population chinoise par exemple. Mais j'imagine que les statistiques sont, à quelques approximations près, plutôt précises.

Merci !

Et bon week-end !

Alx (et je suis très reconnaissant, éternellement on verra héhé)

[Jean-Francois]

Mais cela reste pour moi tout à fait contre-intuitif et réducteur de ne prendre que 1000 personnes pour généraliser à toute la population chinoise par exemple

Pas du tout! La technique de "sondage" du gouvernement chinois est très très au point et (quasi-)infaillible: on prend mille personnes au hasard dans la population. On les fusille en faisant savoir publiquement qu'elles avaient une opinion contraire à ce qui est bon pour le peuple chinois... et, miracle, toute la populatiion à l'opinion qui est bonne pour le peuple donc plus besoin de sondage.

Jean-François

[Christian]

Mais cela reste pour moi tout à fait contre-intuitif et réducteur de ne prendre que 1000 personnes pour généraliser à toute la population chinoise par exemple

Pas du tout! La technique de "sondage" du gouvernement chinois est très très au point et (quasi-)infaillible: on prend mille personnes au hasard dans la population. On les fusille en faisant savoir publiquement qu'elles avaient une opinion contraire à ce qui est bon pour le peuple chinois... et, miracle, toute la populatiion à l'opinion qui est bonne pour le peuple donc plus besoin de sondage.

Jean-François

Leur dernier gros sondage a eu lieu à la Place Tian'anmen, si je me souviens bien... Plusieurs dirigeants de l'équipe statistique on été limogé car ils avaient permis à trop de monde de participer au sondage. Comme il y avait trop de monde pour le sondage, le parti s'est résigné à donner la permission aux sondeurs de faire leur enquête en chars d'assaut.

Christian

[Wooden Ali]

Bien sur, comme le mentionne Denis, plus la louche est grande, plus le taux d'erreur diminue, mais le facteur essentiel, c'est que
le prélèvement doit se faire de façon tout à fait hasardeuse en s'assurant de prélever également dans tous les groupes possibles.

le problème est que c'est ça qui coute cher ! On donne à celui qui fait le sondage, pour pallier aux impossibilités pratiques, un éventail d'échantillons plus grand que celui qui servira. Il a donc la faculté de faire son propre échantillonnage et introduire ainsi un biais non prévu.
On utilise aussi la méthode des quotas :

Méthode d’échantillonnage qui consiste à s’assurer de la représentativité d’un échantillon en lui affectant une structure similaire à celle de la population de base. La méthode des quotas est très utilisée pour les sondages politiques. Dans ce cadre, on s’assure que l’échantillon soit une représentation réduite de la population en âge de voter en terme d’âge, de CSP et éventuellement d’habitat.

Qui présente des avantages mais aussi ses propres biais (les catégories doivent être assez nombreuses et bien définies). Mais plus elles sont nombreuses, plus l'erreur d'échantillonnage à l'intérieur de chacune des catégories est grand si l'on n'augmente pas la taille de l'échantillon global.
Ce sont moins les méthodes qui sont en cause que le désir de tirer les prix au maximum et de tricher avec ce que les mathématiques suggèrent qui sont responsables des flops célèbres dans les prédictions.